Tuned förstärkare-Tutorialspoint

annonser

de typer av förstärkare som vi hittills har diskuterat kan inte fungera effektivt vid radiofrekvenser, även om de är bra på ljudfrekvenser. Förstärkningen av dessa förstärkare är också sådan att den inte kommer att variera beroende på signalens frekvens, över ett brett spektrum., Detta gör att förstärkningen av signalen lika bra över en rad frekvenser och tillåter inte val av viss önskad frekvens samtidigt avvisa de andra frekvenserna.

så, det finns ett behov av en krets som kan välja samt förstärka. Så, en förstärkarkrets tillsammans med ett urval, till exempel en avstämd krets gör en avstämd förstärkare.

Vad är en inställd förstärkare?

avstämda förstärkare är de förstärkare som används för att ställa in. Tuning innebär att välja., Bland en uppsättning frekvenser tillgängliga, om det finns ett behov av att välja en viss frekvens, medan avvisa alla andra frekvenser, kallas en sådan process val. Detta val görs genom att använda en krets som kallas avstämd krets.

När en förstärkarkrets har sin last ersatt av en avstämd krets, kan en sådan förstärkare kallas som en avstämd förstärkarkrets. Den grundläggande avstämda förstärkarkretsen ser ut som visas nedan.

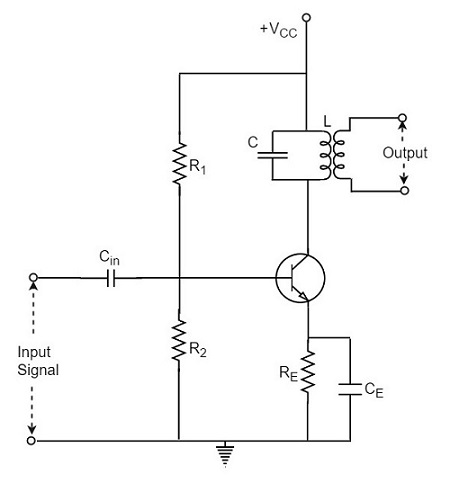
tunerkretsen är ingenting annat än en LC-krets som också kallas resonant eller tankkrets. Den väljer frekvensen., En avstämd krets kan förstärka en signal över ett smalt frekvensband som är centrerad vid resonansfrekvens.

När induktorns reaktans balanserar kondensatorns reaktans, i den inställda kretsen vid någon frekvens, kan en sådan frekvens kallas som resonansfrekvens. Det betecknas med fr.,

formeln för resonans är

$$2 \pi f_L = \frac{1}{2 \pi f_c}$$

$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$

typer av avstämda kretsar

en avstämd krets kan vara serie avstämd krets (serie resonanskrets) eller parallell avstämd krets (parallell resonanskrets) enligt typen av dess resonanskrets.anslutning till huvudkretsen.

Series Tuned Circuit

induktorn och kondensatorn som är anslutna i Serie gör en serie tuned circuit, som visas i följande kretsschema.,

vid resonansfrekvens erbjuder en serie resonanskrets låg impedans som tillåter hög ström genom den. En serie resonanskrets erbjuder allt högre impedans till frekvenserna långt ifrån resonansfrekvensen.

Parallellinställd krets

induktorn och kondensatorn som är anslutna parallellt gör en parallellinställd krets, som visas i nedanstående figur.

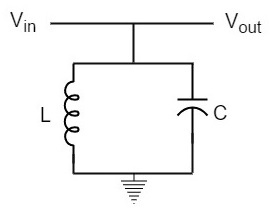
vid resonansfrekvens erbjuder en parallell resonanskrets hög impedans som inte tillåter hög ström genom den., En parallell resonanskrets erbjuder alltmer låg impedans till frekvenserna långt från resonansfrekvensen.

egenskaper hos en Parallellinställd krets

frekvensen vid vilken parallell resonans uppträder (dvs reaktiv komponent i kretsströmmen blir noll) kallas resonansfrekvensen fr. De viktigaste egenskaperna hos en inställd krets är följande.

Impedans

förhållandet mellan matningsspänningen och linjeströmmen är impedansen hos den inställda kretsen., Impedans som erbjuds av LC circuit ges av

$$ \ frac{Supply\: voltage}{Line equation} = \frac{V}{i}$$

vid resonans ökar linjeströmmen medan impedansen minskar.

nedanstående figur representerar impedanskurvan för en parallell resonanskrets.

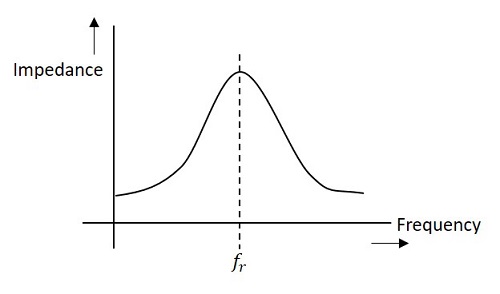
impedansen hos kretsen minskar för värdena ovan och under resonansfrekvensen fr. Därför är valet av en viss frekvens och avstötning av andra frekvenser möjligt.,

To obtain an equation for the circuit impedance, let us consider

Line Current $I = I_L cos \phi$

$$\frac{V}{Z_r} = \frac{V}{Z_L} \times \frac{R}{Z_L}$$

$$\frac{1}{Z_r} = \frac{R}{Z_L^2}$$

$$\frac{1}{Z_r} = \frac{R}{L/C} = \frac{C R}{L}$$

Since, $Z_L^2 = \frac{L}{C}$

Therefore, circuit impedance Zr is obtained as

$$Z_R = \frac{L}{C R}$$

Thus at parallel resonance, the circuit impedance is equal to L/CR.,

Kretsström

vid parallell resonans ges kretsen eller linjeströmmen I av den applicerade spänningen dividerad med kretsens impedans Zr, dvs

Linjeström $i = \frac{V}{Z_r}$

där $Z_r = \frac{L}{C r}$

eftersom ZR är mycket hög, linjen nuvarande jag kommer att vara mycket liten.

kvalitetsfaktor

för en parallell resonanskrets bestämmer skärpan i resonanskurvan selektiviteten. Ju mindre spolens motstånd desto skarpare kommer resonanskurvan att vara., Därför bestämmer spolens induktiva reaktans och motstånd kvaliteten på den inställda kretsen.

förhållandet mellan spolens induktiva reaktans vid resonans till dess motstånd kallas kvalitetsfaktor. Det betecknas med Q.

$ $ Q = \ frac{X_L}{R} = \frac{2 \ pi f_r L}{R}$$

ju högre värdet på Q, desto skarpare resonanskurvan och desto bättre blir selektiviteten.

fördelar med inställda förstärkare

Följande är fördelarna med inställda förstärkare.,

användningen av reaktiva komponenter som l och C, minimerar strömförlusten, vilket gör de inställda förstärkarna effektiva.
selektivitet och förstärkning av önskad frekvens är hög, genom att ge högre impedans vid resonansfrekvens.
en mindre samlare leverans VCC skulle göra, på grund av dess lilla motstånd i parallell avstämd krets.

det är viktigt att komma ihåg att dessa fördelar inte är tillämpliga när det finns en hög resistiv samlarbelastning.,

frekvensrespons för avstämd förstärkare

för att en förstärkare ska vara effektiv bör förstärkningen vara hög. Denna spänningsförstärkning beror på β, ingångsimpedans och kollektorbelastning. Samlarbelastningen i en avstämd förstärkare är en avstämd krets.

spänningsförstärkningen hos en sådan förstärkare ges av

spänningsförstärkning = $\frac{\beta Z_C}{Z_{in}}$

där ZC = effektiv samlarbelastning och Zin = förstärkarens ingångsimpedans.

värdet på ZC beror på frekvensen hos den inställda förstärkaren., Eftersom ZC är maximal vid resonansfrekvens är förstärkarens vinst maximal vid denna resonansfrekvens.

bandbredd

frekvensområdet vid vilket spänningsförstärkningen hos den inställda förstärkaren faller till 70,7% av den maximala förstärkningen kallas dess bandbredd.

frekvensområdet mellan f1 och f2 kallas som bandbredd för den inställda förstärkaren. Bandbredden hos en avstämd förstärkare beror på Q i LC-kretsen dvs vid skärpan av frekvensrespons. Värdet av Q och bandbredden är omvänt proportionella.,

figuren nedan beskriver bandbredd och frekvensrespons för den inställda förstärkaren.

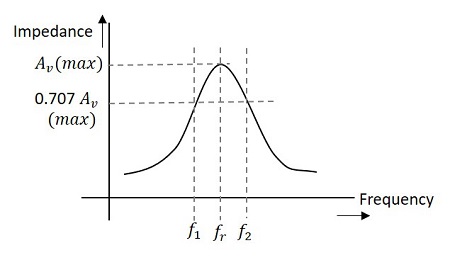
förhållandet mellan Q och bandbredd

kvalitetsfaktorn Q för bandbredden definieras som förhållandet mellan resonansfrekvens och bandbredd, dvs

$$Q = \frac{f_r}{bw}$$

i allmänhet har en praktisk krets sitt Q-värde större än 10.,

under detta tillstånd ges resonansfrekvensen vid parallell resonans av