typer forsterkere som vi har diskutert så langt ikke kan arbeide effektivt på radio frekvenser, selv om de er gode på lyd-frekvenser. Også, få av disse forsterkerne er slik at det ikke vil variere i henhold til frekvensen på signalet, over et bredt spekter., Dette gjør at forsterkning av signalet like godt over et spekter av frekvenser og tillater ikke det utvalget av særlig ønsket frekvens, mens avvise andre frekvenser.
Så, det oppstår et behov for en krets som kan velge samt forsterke. Så, en forsterker sammen med et utvalg, for eksempel en innstilt krets gjør en Innstilt forsterker.
Hva er en Innstilt Forsterker?
Tilpasset forsterkere forsterkere som er ansatt i den hensikt av tuning. Tuning betyr å velge., Blant et sett av frekvenser tilgjengelig, hvis det oppstår et behov for å velge en bestemt frekvens, mens avvise alle andre frekvenser, slik at en prosess som kalles Valg. Dette utvalget er gjort ved hjelp av en krets kalt Stemt krets.
Når en forsterker har sin laste erstattet av en innstilt krets, for eksempel en forsterker kan kalles som en Innstilt forsterker. Den grunnleggende innstilt forsterker ser ut som vist nedenfor.
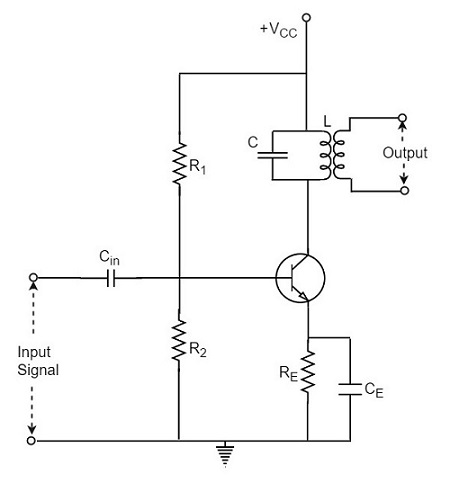
tuner krets er ingenting, men en LC-krets som også kalles som betydningsfulle eller tank krets. Det velger frekvens., En innstilt krets er i stand til å forsterke et signal over et smalt bånd av frekvenser som er sentrert på resonansfrekvens.
Når reaktans av spole balanserer reaktans av kondensatoren, i den justerte kursen på noen frekvens, slik en frekvens kan bli kalt inn som resonansfrekvens. Det er merket av fr.,
formelen for resonans er
$$2 \pi f_L = \frac{1}{2 \pi f_c}$$
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
Typer Innstilt Kretser
En innstilt krets kan bli en Serie stemt krets (Serie resonant krets) eller Parallell stemt krets (parallell resonant krets) i henhold til type av sin tilknytning til den største kretsen.
– Serien Stemt Krets
spole og kondensator koblet i serie lage en serie stemt krets, som vist i følgende koblingsskjema.,

På resonansfrekvens, en serie resonant krets tilbyr lav impedans som gir høy strøm gjennom det. En serie resonant krets tilbyr stadig høy impedans for frekvensene langt fra resonansfrekvens.
Parallell Stemt Krets
spole og kondensator koblet i parallell gjøre en parallell stemt krets som vist i figur nedenfor.
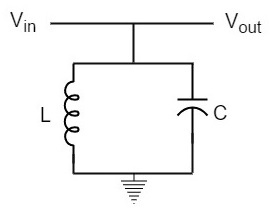
På resonansfrekvens, en parallell resonant krets tilbyr høy impedans som ikke tillater høy strøm gjennom det., En parallell resonant krets har i økende grad med lav impedans for frekvensene langt fra resonansfrekvens.
Egenskaper av en Parallell Stemt Krets
Den frekvensen som parallell resonans oppstår (dvs. reaktive komponenten av kretsen gjeldende blir null) kalles resonans frekvensen fr. De viktigste egenskapene til en innstilt kretsen er som følger.
Impedans
forholdet mellom spenning til gjeldende linje er impedansen på stemt krets., Impedans som tilbys av LC-krets er gitt ved
$$\frac{Tilførsel \: spenning}{Line equation} = \frac{V}{I}$$
Ved resonans, line strøm øker, mens impedans synker.
nedenfor figur representerer impedans kurve av en parallell resonans krets.
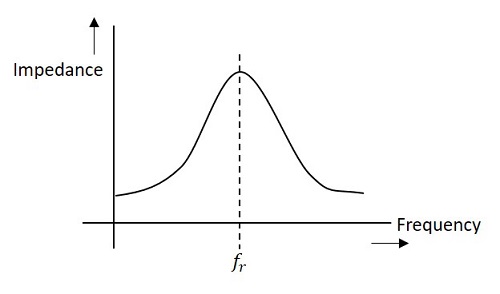
Impedansen i kretsen synker for verdier over og under resonansfrekvens fr. Derfor valg av en bestemt frekvens og avvisning av andre frekvenser er mulig.,
To obtain an equation for the circuit impedance, let us consider
Line Current $I = I_L cos \phi$
$$\frac{V}{Z_r} = \frac{V}{Z_L} \times \frac{R}{Z_L}$$
$$\frac{1}{Z_r} = \frac{R}{Z_L^2}$$
$$\frac{1}{Z_r} = \frac{R}{L/C} = \frac{C R}{L}$$
Since, $Z_L^2 = \frac{L}{C}$
Therefore, circuit impedance Zr is obtained as
$$Z_R = \frac{L}{C R}$$
Thus at parallel resonance, the circuit impedance is equal to L/CR.,
Krets Gjeldende
Ved parallell resonans, kretsen eller linje dagens jeg er gitt ved søkte spenning delt på kretsen impedans Zr dvs.,
Gjeldende Linje $I = \frac{V}{Z_r}$
Hvor $Z_r = \frac{L}{R}$
Fordi Zr er svært høy, linje dagens jeg vil være svært liten.
Kvalitet Faktor
For en parallell resonans krets, skarpheten resonans kurve bestemmer selektivitet. Jo mindre motstand av spolen, skarpere resonans kurven vil være., Derav induktiv reaktans og resistans av spolen fastslå kvaliteten på stemt krets.
forholdet mellom induktiv reaktans av spolen på resonans til sin motstand er kjent som Quality faktor. Det er merket med Q.
$$Q = \frac{X_L}{R} = \frac{2 \pi f_r L}{R}$$
Jo høyere verdi av Q, skarpere resonans kurve og bedre selektivitet vil være.
Fordeler med Tilpasset Forsterkere
følgende fordeler av tuned forsterkere.,
-
bruk av reaktive komponenter som L og C, minimerer tapet av kraft, noe som gjør den innstilte forsterkere effektiv.
-
selektivitet og forsterkning av ønsket frekvens er høy, ved å gi høyere impedans på resonansfrekvens.
-
En mindre collector tilførsel VCC ville gjøre, på grunn av sin lite motstand i parallell stemt krets.
Det er viktig å huske at disse fordelene er ikke aktuelt når det er en høy resistiv samler inn.,
Frekvensrespons Innstilt Forsterker
For en forsterker til å bli effektiv, sin gevinst bør være høy. Denne spenningen får, avhenger av β, inngangsimpedans og samler inn. Samleren legg i en innstilt forsterker er en innstilt krets.
spenning gevinst på slik en forsterker er gitt ved
Spenning gevinst = $\frac{\beta Z_C}{Z_{i}}$
Hvor ZC = effektiv collector legg og Zin = inngangsimpedans av forsterkeren.
verdien av ZC avhenger av frekvensen av innstilt forsterker., Som ZC er maksimalt resonansfrekvens, den vinning av forsterker er maksimalt dette resonansfrekvens.
Båndbredde
spekter av frekvenser der spenningen få av innstilt forsterker faller til 70.7% av maksimal gevinst er kalt sin Båndbredde.
spekter av frekvenser mellom f1 og f2 er kalt til båndbredde av innstilt forsterker. Båndbredden på en innstilt forsterker avhenger av Q av LC-krets vil si, på skarpheten på frekvens respons. Verdien av Q og båndbredde er omvendt proporsjonal.,
figuren nedenfor detaljer båndbredde og frekvens respons av innstilt forsterker.
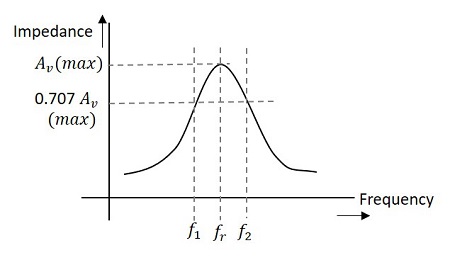
Forhold mellom Q og Båndbredde
kvalitetsfaktor Q av båndbredde er definert som forholdet mellom resonansfrekvens til båndbredde, dvs.,
$$Q = \frac{f_r}{BW}$$
generelt en praktisk krets har sin Q-verdi som er større enn 10.,
Under denne tilstanden, resonans frekvensen på parallell resonans er gitt ved
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
















Legg igjen en kommentar