vektorer är mycket användbara inom vetenskapen för att beskriva allt som har både en riktning och en magnitud. De är vanligtvis ritade med hjälp av spetsiga pilar, vars längd kommer att representera vektorns storlek. En quarterback pass är det enkla exemplet eftersom det har riktningen vanligtvis någonstans downfield och en magnitud. Ibland måste vi hantera två vektorer tillsammans som arbetar på något objekt. I sådana fall är vinklar mellan dessa vektorer viktiga., Detta ämne kommer att förklara vinkeln mellan två vektorer formel samt exempel. Låt oss lära oss det!
begreppet vektorer
utanför fältet kan vektorer användas för att representera valfritt antal fysiska objekt eller aktiviteter. Exempelvis. Vind är till exempel en vektorkvantitet. Det beror på att den på en viss plats har en riktning såväl som storleken. Vi kan göra en karta över luftflödet när som helst, då, genom att dra vindvektorerna för ett antal olika geografiska platser.
många egenskaper hos rörliga objekt är också typ av vektorer., I biljardboll beskriver dess hastighetsvektor sin rörelse. Det visar riktningen för vektorpilen markerar som rörelseriktningen, och vektorns längd representerar bollens hastighet.
biljardbollens momentum är också ett exempel på vektorkvantitet. Eftersom det är lika med mass gånger hastighet. Därför momentumvektorn av kulpunkterna i samma riktning som dess hastighetsvektor. Och momentumvektorns storlek kommer att vara multiplikationsprodukten av bollens hastighet och dess massa.,
När det gäller matematik är en vektor ett objekt som har en definierbar magnitud och riktning. Eftersom vektorer inte är desamma som standardlinjer eller former måste vi använda några speciella formler för att hitta vinklar mellan dem.
formeln för vinkeln mellan två vektorer
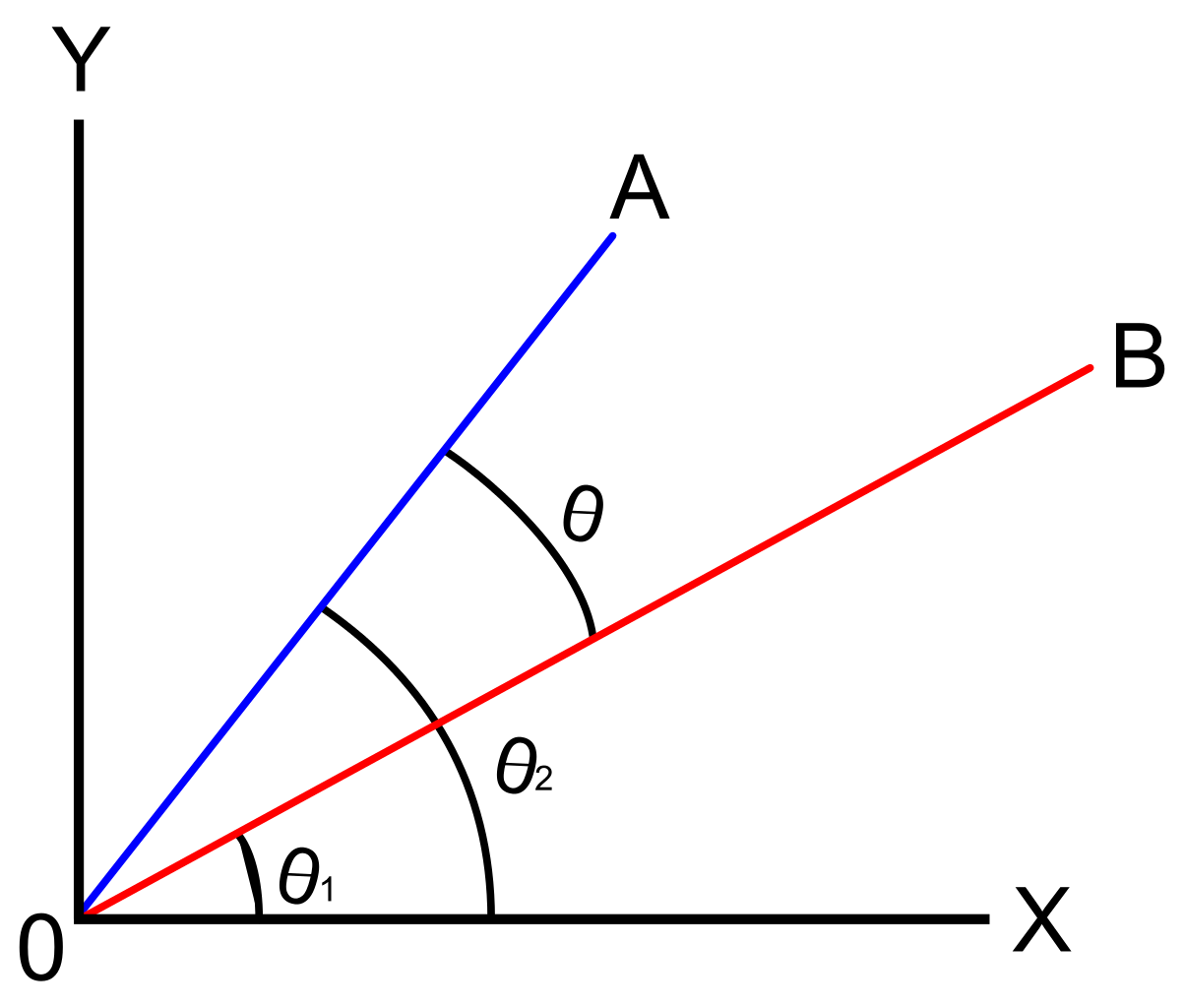
vinkeln mellan två vektorer kommer att skjutas upp med en enda punkt, som kallas den kortaste vinkeln vid vilken vi måste vända en av vektorerna till positionen för samriktning med en annan vektor.,
diskussionen om vektorernas riktningsvinklar fokuserar på att hitta vinkeln på en vektor med avseende på den positiva x-axeln. Detta kommer att fokusera på vinkeln mellan två vektorer i standardpositionen. En vektor sägs vara i standardläge om dess ursprungliga punkt är ursprunget (0, 0).
om de två vektorerna antas som A och B definieras punkten som A .B. låt oss anta att dessa två vektorer är åtskilda av angle \(\theta\). För att veta vad som är vinkelmätningen kommer vi att lösa med hjälp av formeln:
vi känner till punktprodukten:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{B}|cos\theta\)
nu är vinkeln mellan två vektorer formel:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}} {|\vec{a}||\vec{b}|}\)
där \\ (theta\) är vinkeln mellan A-och B-vektorer.
löste exempel på vinkel mellan två vektorer formel
Q. 1: beräkna vinkeln mellan två vektorer 3i + 4j – k och 2i – j + k.
lösning: Låt,
a = 3i + 4j – k och
b = 2i – j + K
vi definierar punktprodukten som:
a .b = (3i + 4j – k).(2i – j + k)
















Lämna ett svar