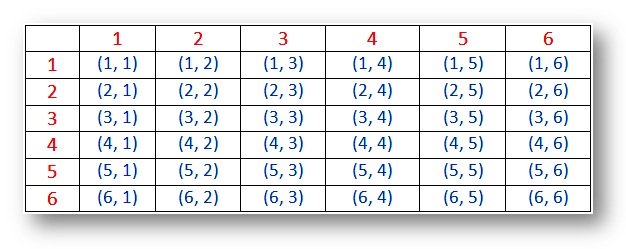
Sannolikhet för att rulla två tärningar med sexsidiga dotsså som 1, 2, 3, 4, 5 och 6 punkter i varje tärning.

när två tärningar kastas samtidigt kan antalet händelser vara 62 = 36 eftersom varje tärning har 1 till 6 nummer på sina ansikten. Därefter visas de möjliga resultaten i nedanstående tabell.,
Probability-Sample space for two dice (outcomes):
notera:
(i) utfallet (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) och (6, 6) kallas dubbletter.
(ii) paret (1, 2) och (2, 1) är olika resultat.
utarbetade problem med Sannolikhet för att rulla två tärningar:
1. Två tärningar rullas. Låt a, b, c vara händelserna för att få en summa av 2, en summa av 3 och en summa av 4 respektive., Visa sedan att
(i) A är en enkel händelse
(ii) B och C är sammansatta händelser
(iii) A och B är ömsesidigt exklusiva
lösning:
klart, vi har
a = {(1, 1)}, B = {(1, 2), (2, 1)} och C = {(1, 3), (3, 1), (2, 2)}.
(i) Eftersom A består av en enda provpunkt, är det en enkel händelse.
(ii) eftersom både B och C innehåller mer än en provpunkt är var och en av dem en sammansatt händelse.
(iii) eftersom A och B är ömsesidigt uteslutande.
2. Två tärningar rullas., A är händelsen att summan av siffrorna som visas på de två tärningarna är 5, och B är händelsen att minst en av tärningarna visar upp en 3.
är de två händelserna (i) ömsesidigt uteslutande, (ii) uttömmande? Ge argument till stöd för ditt svar.
lösning:
När två tärningar rullas har vi n(S) = (6 × 6) = 36.
nu, en = {(1, 4), (2, 3), (4, 1), (3, 2)}, och
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A = {(2, 3), (3, 2)} ≠ ∅.
därför är A och B inte ömsesidigt uteslutande.,
(ii) även, A B B S.
därför är A och B inte uttömmande händelser.
fler exempel relaterade till frågorna om sannolikheterna för att kasta två tärningar.
3. Två tärningar kastas samtidigt.,) få en dubblett
(v) få en summa av 8
(vi) få summan delbar med 5
(vii) få summan av minst 11
(viii) få en multipel av 3 som summan
(ix) få totalt minst 10
(x) få ett jämnt antal som summan
(x) få ett jämnt antal som summan
(Xi) att få ett primtal som summan
(XII) att få en dubblett av jämna nummer
(XIII) att få en multipel av 2 på en dö och en multipel av 3 på den andra dö
lösning:
två olika tärningar kastas samtidigt som nummer 1, 2, 3, 4, 5 och 6 på deras ansikten., Vi vet att i en enda kastad av två olika tärningar är det totala antalet möjliga resultat (6 × 6) = 36.
(i) få sex som en produkt:
låt E1 = händelse av att få sex som en produkt. Antalet vars produkt är sex kommer att vara E1 = = 4
därför Sannolikhet ofgetting ’sex som en produkt’
antal gynnsamma resultat
P(E1) = Totalt antal möjliga resultat
= 4/36
= 1/9
(ii) få summan ≤ 3:
låt E2 = händelse av att få summan ≤ 3., Antalet vars summa ≤ 3 kommer att vara E2 = = 3
därför Sannolikhet ofgetting ’sum ≤ 3’
antal gynnsamma resultat
P (E2)= Totalt antal möjliga resultat
= 3/36
= 1/12
(iii) få summan ≤ 10:
låt E3 = händelse av att få summan ≤ 10. Antalet vars summa ≤ 10 kommer att vara E3 =
= 33
därför Sannolikhet ofgetting ’sum ≤ 10’
antal gynnsamma resultat
p(E3) = Totalt antal möjliga resultat
= 33/36
= 11/12
(iv)få en dubblett:låt E4 = händelse av att få en dubblett., Antalet som doublet kommer att vara E4 = = 6
därför sannolikheten för att få ’en doublet’
antal gynnsamma resultat
P (E4)= Totalt antal möjliga resultat
= 6/36
= 1/6
(v) få en summa av 8:
låt E5 = händelse av att få en summa av 8. Antalet som är en summa av 8 kommer att vara E5 = = 5
därför Sannolikhet ofgetting ’en summa av 8’
antal gynnsamma resultat
P (E5) = Totalt antal möjliga resultat
= 5/36
(vi) få summan delbar med 5:
låt E6 = händelse av att få summan delbar med 5., Antalet vars summa delbar med 5 kommer att vara E6 = = 7
därför Sannolikhet ofgetting ’summan delbar med 5’
antal gynnsamma resultat
P(E6) = Totalt antal möjliga resultat
= 7/36
(vii)få summan av minst 11:
låt E7 = händelse av att få summan av minst 11. Händelserna i summan av alleast 11 kommer att vara E7 = = 3
därför Sannolikhet ofgetting ’summan av alleast 11’
antal gynnsamma resultat
P (E7)= Totalt antal möjliga resultat
= 3/36
= 1/12
(viii) få amultiple av 3 som summan:
låt E8 = händelse av att få en multipel av 3 som summan., Händelserna i en multipel av 3 som summan kommer att vara E8 = = 12
därför Sannolikhet ofgetting ’en multipel av 3 som summan’
antal gynnsamma resultat
P (E8)= Totalt antal möjliga resultat
= 12/36
= 1/3
(ix) att få en total av minst 10:
låt E9 = händelse av att få totalt minst 10., Händelserna i totalt minst 10 kommer att vara E9 = = 6
därför Sannolikhet ofgetting ’totalt minst 10’
antal gynnsamma resultat
P (E9)= Totalt antal möjliga resultat
= 6/36
= 1/6
(x) få en jämntal som summan:
låt E10 = händelse av att få ett jämnt tal som summan., Händelserna i ett jämnt tal som summan kommer att vara E10 = = 18
därför Sannolikhet ofgetting ’ ett jämnt tal som summan
antal gynnsamma resultat
P (E10)= Totalt antal möjliga resultat
= 18/36
= 1/2
(xi) att få ett primenumber som summan:
låt E11 = händelse av att få ett primtal som summan., Händelserna i ett primtal som summan kommer att vara E11 = = 15
därför Sannolikhet ofgetting ’ett primtal som summan’
antal gynnsamma resultat
P (E11)= Totalt antal möjliga resultat
= 15/36
= 5/12
(xii) få adoublet av jämna nummer:
låt E12 = händelse av att få en dubblett av jämna nummer., Händelserna i en dubblett med jämna nummer kommer att vara E12 = = 3
därför sannolikheten för attfå ’en dubblett av jämna nummer’
antal gynnsamma resultat
P(E12) = Totalt antal möjliga resultat
= 3/36
= 1/12
(xiii) få amultiple av 2 på en dö och en multipel av 3 på den andra dö:
låt E13 = händelse av att få en multipel av 2 på en dö och en multipel av av 3 på den andra dör., Händelserna i en multipel av 2 på en dö och en multipel av 3 på den andra dö kommer att vara E13 = = 11
därför sannolikheten ofgetting ’en multipel av 2 på en dö och en multipel av 3 på den andra dö’
antal gynnsamma resultat
P (E13)= Totalt antal möjliga resultat
= 11/36
4. Två gånger kastas. Hitta (i) oddsen för att få summan 5, och (ii) theodds mot att få summan 6.
lösning:
vi vet att i en enda kastad av två dör är det totala antalet möjliga resultat (6 × 6) = 36.
Låt oss vara provutrymmet. Sedan,n(S) = 36.,
(i) oddsen för att få summan 5:
låt E1 vara händelsen att få summan 5. Sedan
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)} (E1) = 4
därför, p(E1) = n(e1)/n(s) = 4/36 = 1/9
för e1 = p(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) oddsen mot att få summan 6:
låt E2 vara händelsen att få summan 6. Sedan
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)} (E2) = 5
därför, p(E2) = n(E2)/n(s) = 5/36
mot E2 = /p(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Två tärningar, en blå och en orange, rullas samtidigt. Hitta sannolikheten att få
(i) lika tal på båda
(ii) två tal som visas på dem vars summa är 9.,
lösning:
de möjliga resultaten är
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
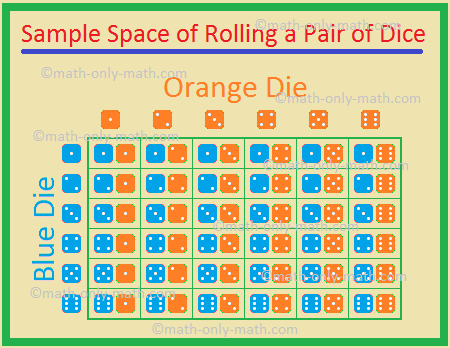
därför totalt antal möjliga resultat = 36.,
(i) antal gynnsamma resultat för händelsen E
= antal resultat som har lika många siffror på båda tärningarna
= 6 .
så, per definition, p(e) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) antal gynnsamma utfall för händelsen F
= antal utfall där två tal som visas på dem har summan 9
= 4 .
således per definition, p(f) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
dessa exempel kommer att hjälpaus att lösa olika typer av problem baserat på Sannolikhet för rollingtwo tärningar.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Lämna ett svar