När vinklarna i en triangel inte lägger till upp till 180 grader

1. Inledning

lägger vinklarna på en triangel upp till 180 grader eller $\pi$ radianer? Svaret är ”ibland Ja, ibland Nej”. Är detta en viktig fråga? Ja, eftersom det leder till en förståelse för att det finns olika geometrier baserade på olika Axiom eller ”regler i spelet geometri”. Är det en meningsfull fråga? Tja Nej, åtminstone inte förrän vi har kommit överens om innebörden av orden ”vinkel” och ”Triangle”, inte förrän vi vet spelets regler., I den här artikeln diskuterar vi kortfattat de underliggande axiomerna och ger ett enkelt bevis på att summan av vinklarna i en triangel på ytan av en enhetssfär inte är lika med $\pi$ men till $\pi$ plus triangeln. Vi ska använda det faktum att ytan på en enhetssfär är $4\pi$.

2. The Big Theorem

innan vi kan säga vad en triangel är måste vi komma överens om vad vi menar med poäng och linjer. Vi arbetar med sfärisk geometri (bokstavligen geometri på ytan av en sfär)., I denna geometri är utrymmet sfärens yta; punkterna är punkter på den ytan, och linjen med kortast avstånd mellan två punkter är den stora cirkeln som innehåller de två punkterna. En stor cirkel (somekvatorn) skär sfären i två lika halvkärmar. Denna geometri har uppenbara tillämpningar på avstånd mellan platser och luftvägar på jorden.,

roterande sfär som visar stor cirkel

vinkeln mellan två stora cirklar vid en punkt P är den euklidiska vinkeln mellan cirkelns riktningar (eller strikt mellan tangenterna till cirklarna vid P). Detta medför inga svårigheter att navigera på jorden eftersom vi vid varje given tidpunkt tänker på vinkeln mellan två riktningar som om jorden var platt vid den punkten.

en lune är en del av sfärens yta som avgränsas av två stora cirklar som möts vid antipodala punkter., Vi först överväga området av en lune och sedan införa en annan stor cirkel som delar lune i trianglar.

roterande sfär som visar 4 lunes

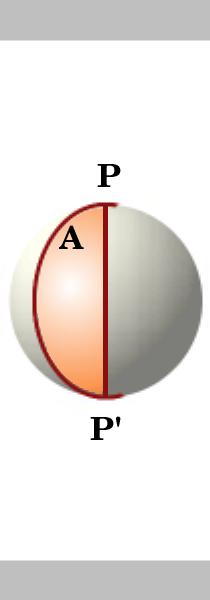
Lemma.

området för en lune på en cirkel av radie enhet är dubbelt dess vinkel, det vill säga om vinkeln på lune är en då dess område är 2A. två stora cirklar skär vid antipodala punkter P och P’ dela sfären i 4 lunes. Ytan på en enhetssfär är $ 4 \ pi$.,

lunes områden är proportionella mot deras vinklar vid P så att området för en lune med vinkel A är

${\frac{a}{2\pi}\times {4\pi}= {2A}}$

Övning 1.

vilka områden är de andra 3 lunesna? Lägger dina 4 områden upp till $ 4 \ pi$?

kontrollera dina svar här .

sidorna av en triangel ABC är segment av tre stora cirklar som faktiskt skär ytan av sfären i åtta sfäriska trianglar. Mellan de två stora cirklarna genom punkten A finns det fyra vinklar., Vi märker vinkeln inuti triangeln ABC som vinkel A, och på samma sätt de andra vinklarna i triangeln ABC som vinkel B och vinkel C.

roterande sfär som visar 8 trianglar

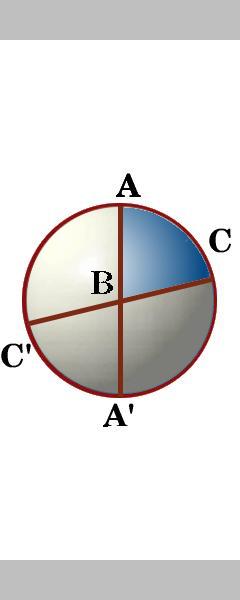
Övning 2

rotera sfären kan du namnge de åtta trianglarna och säga om någon av dem har samma område? Kontrollera dina svar här .

Sats.

överväga en sfärisk triangel ABC på enhetssfären med vinklar A, B och C. då är området triangeln ABC

a + b + c – $\pi$.,

diagrammet visar en vy som tittar ner på halvklotet som har linjen genom AC som dess gräns. Regionerna markerade Område 1 och Område 3 är lunes med vinklar a respektive C. Tänk på lunes genom B och B’. Triangeln ABC är kongruent till triangeln A ’B’ C ’så fluga formade skuggade område, märkt område 2, som är summan av de områden av trianglarna ABC och A’BC’, är lika med området för lune med vinkel B, som är lika med 2B.,

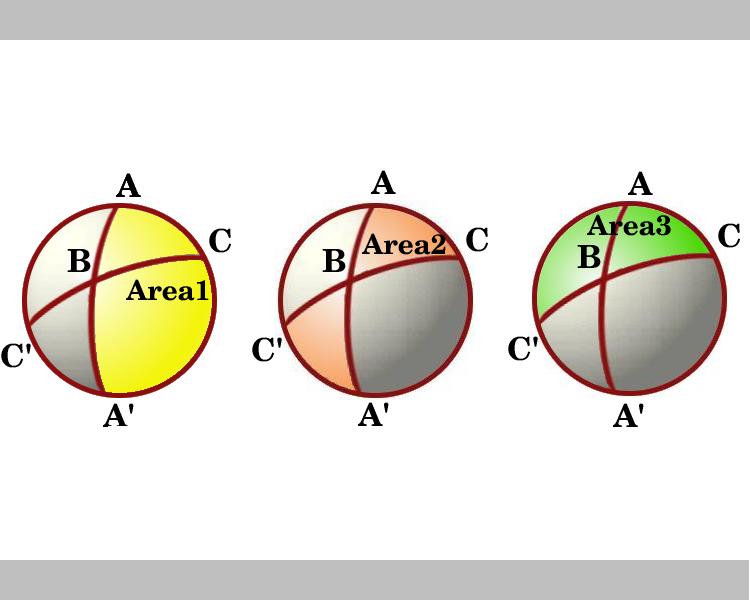
så i diagrammet ser vi områdena med tre lunes och med hjälp av lemma är dessa:

Område 1 = 2A
område 2 = 2b
område 3 = 2C

när vi lägger upp dessa tre områden inkluderar vi triangelområdet ABC tre gånger., Hence

3., Icke-euklidisk geometri

Ibland är revolutionära upptäckter Ingenting annat än att faktiskt se vad som har varit under våra näsor hela tiden. Detta var fallet över upptäckten av icke-euklidisk geometri under nittonde århundradet. Under 2000 år efter att Euclid skrev sina ”element” i 325 f. Kr. försökte folk bevisa det parallella postulatet som en teorem i geometrin från de andra axiomerna men misslyckades alltid och det är en lång historia., Samtidigt matematiker använde sfärisk geometri hela tiden, en geometri som lyder de andra Axiom av euklidisk geometri och innehåller många av samma satser, men där den parallella postulat inte håller. Hela tiden hade de ett exempel på en icke-euklidisk geometri under sina näsor.

Tänk på en linje l och en punkt P inte på L. Den stora frågan är: ”hur många linjer kan dras genom P parallellt med L?`I euklidisk geometri är svaret ”exakt ett” och det här är en version av parallell postulatet., Om summan av vinklarna för varje triangel i geometrin är $\pi$ radianer så håller parallell postulatet och vice versa, de två egenskaperna är likvärdiga.

i sfärisk geometri skiljer sig de grundläggande axiomerna som vi antar (spelets regler) från euklidisk geometri – det här är en icke-euklidisk geometri. Vi har sett att trianglarnas vinklar i sfärisk geometri inte alltid lägger till upp till $\pi$ radianer så vi skulle inte förvänta oss att det parallella postulatet håller., I sfärisk geometri är de raka linjerna (linjer med kortaste avstånd eller geodesik)stora cirklar och varje linje i geometrin skär varannan linje i två punkter. Svaret på den stora frågan om paralleller är ” om vi har en linje l och en punkt P inte på L så finns det inga linjer genom P parallellt med linjen L.,”

de grekiska matematikerna (till exempel Ptolemy C 150) beräknade mätningarna av rätvinkliga sfäriska trianglar och arbetade med formler av sfäriska trigonometri och arabiska matematiker (till exempel Jabir ibn Aflah C 1125 och Nasir ed-din C 1250) förlängde arbetet ytterligare. Formeln som diskuterades i denna artikel upptäcktes av Harriot 1603 och publicerades av Girard 1629. Ytterligare aspekter av ämnet utvecklades av Saccerhi (1667-1733).,

allt detta gick till stor del un-märkt av 1800-talet upptäckare av hyperbolisk geometri, vilket är en annan icke-euklidisk geometri där parallell postulat inte håller. I sfärisk geometri (även kallad elliptisk geometri) lägger trianglarnas vinklar upp till mer än $\pi$ radianer och i hyperbolisk geometri lägger trianglarnas vinklar upp till mindre än $\pi$ radianer.

för vidare läsning se artikeln av Alan Beardon ’ hur många geometrier finns det?”och artikeln av Keith Carne ”Strange Geometries”., Det finns några praktiska aktiviteter som du kan prova själv att utforska dessa geometrier ytterligare som finns på http://nrich.maths.org/MOTIVATE/conf8/index.html