Dela på

innehåll (Klicka för att hoppa till det avsnittet):

  1. allt om…
    • medelvärde
    • läge
    • median
  2. hur man hittar medelvärdet, medianen och läget för hand.
  3. hitta medelvärdet, medianen och läget med teknik:
    • SPSS
    • TI83

översikt

fastnat på hur man hittar medelvärdet, median,& läge i statistik?,

  1. medelvärdet är medelvärdet för en datamängd.
  2. läget är det vanligaste numret i en datamängd.
  3. medianen är mitten av uppsättningen siffror.

av de tre är medelvärdet det enda som kräver en formel. Jag gillar att tänka på det i den andra ordlistan bemärkelse (som i, det är elakt i motsats till nice!). Det beror på att, jämfört med de andra två, det är inte så lätt att arbeta med.,


Tips för att komma ihåg skillnaden

har du problem med att komma ihåg skillnaden mellan medelvärdet, medianen och läget? Här är några tips som kan hjälpa. Du kan också kolla in handledarna på Chegg.com (din första 30 minuter är gratis!).

  • ”a la mode” är ett franskt ord som betyder fashionabla ; det hänvisar också till ett populärt sätt att servera glass. Så ”Mode” är den mest populära eller fashionabla medlemmen i en uppsättning siffror. Word-läget är också som de flesta.,
  • ” Mean ”kräver att du gör aritmetik (lägger till alla nummer och delar) så det är” mean ” en.
  • ”Median” har samma antal bokstäver som ”mitten”.

är fortfarande inte säker på vad skillnaden är mellan de tre? Titta på videon eller läs vidare för mer info:

vänligen acceptera statistik, marknadsföringscookies för att titta på den här videon.

medelvärdet

medelvärde mot Median
medelvärde mot, Genomsnittlig
specifik ”betyder” som vanligen används i statistik
andra typer

medelvärde vs Median

båda är mått på var mitten av en datauppsättning ligger (kallas ”Central tendens” i statistik), men de är vanligtvis olika siffror. Ta till exempel den här listan med siffror: 10, 10, 20, 40, 70.

  • medelvärdet (informellt, ”medelvärdet”) hittas genom att lägga till alla nummer tillsammans och dividera med antalet objekt i uppsättningen: 10 + 10 + 20 + 40 + 70 / 5 = 30.
  • medianen hittas genom att beställa uppsättningen från lägsta till högsta och hitta den exakta mitten., Medianen är bara mittnumret: 20.

Ibland kommer de två att vara samma nummer. Till exempel har datauppsättningen 1, 2, 4, 6, 7 ett medelvärde för 1 + 2 + 4 + 6 + 7 / 5 = 4 och en median (en mitten) av 4.

betyder vs genomsnitt: Vad är skillnaden?

När du först började i matematik lärde du dig förmodligen att ett genomsnitt var ett ”medelvärde” för en uppsättning siffror. Du lagt upp siffrorna, dividerat med antalet objekt du kan och voila! du får genomsnittet. Till exempel är medelvärdet 10, 5 och 20:

10 + 6 + 20 = 36 / 3 = 12.,

du började studera statistik och helt plötsligt kallas ”genomsnittet” nu medelvärdet. Vad var det som hände? Svaret är att de har samma betydelse (de är synonymer).

som sagt, tekniskt är ordet medelvärdet kort för det aritmetiska medelvärdet. Vi använder olika ord i statistik, eftersom det finns flera olika typer av medel, och de gör alla olika saker.

specifik ”betyder” vanligen används i statistik

Du kommer förmodligen att stöta på dessa i din statistik klass., De har mycket smala betydelser:

  • medelvärde för provtagningsfördelningen: används med sannolikhetsfördelningar, särskilt med Central Limit-Sats. Det är ett genomsnitt av en uppsättning distributioner.
  • prov medelvärde: medelvärdet i ett prov.
  • Population mean: medelvärdet i en population.

Kenney, J. F. och Hålla, E. S. Matematik, Statistik, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.

andra typer

det finns andra typer av medel, och du använder dem i olika grenar av matematik., De flesta har mycket smala applikationer till områden som ekonomi eller fysik; om du är i elementär statistik du förmodligen inte kommer att arbeta med dem.

det här är några av de vanligaste typerna du stöter på.

  1. vägt medelvärde.
  2. harmoniska medelvärde.
  3. geometriskt medelvärde.
  4. aritmetiskt geometriskt medelvärde.
  5. Root-Mean Square menar.
  6. Heronian menar.
  7. grafiskt medelvärde

  1. vägt medelvärde

    dessa är ganska vanliga i statistiken, särskilt när man studerar populationer., I stället för att varje datapunkt bidrar lika till det slutliga genomsnittet bidrar vissa datapunkter mer än andra. Om alla vikter är lika, kommer detta att motsvara det aritmetiska medelvärdet. Det finns vissa omständigheter när detta kan ge felaktiga uppgifter, vilket Simpsons Paradox visar.

  2. harmoniska medelvärde

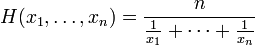
    den harmoniska formeln.

    för att hitta den:

    1. Lägg till fram och återgående siffror i uppsättningen., För att hitta en ömsesidig, vänd fraktionen så att täljaren blir nämnaren och nämnaren blir täljaren. Till exempel är den ömsesidiga 6/1 1/6.
    2. dela svaret med antalet objekt i uppsättningen.
    3. ta det ömsesidiga resultatet.

    det harmoniska medelvärdet används ganska mycket i fysiken. I vissa fall med priser och nyckeltal ger det ett bättre genomsnitt än det aritmetiska medelvärdet. Du hittar också användningsområden i geometri, Ekonomi och datavetenskap.,

  3. geometriskt medelvärde


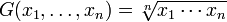
    denna typ har mycket smala och specifika användningsområden inom finans, samhällsvetenskap och teknik. Till exempel, låt oss säga att du äger aktier som tjänar 5% det första året, 20% det andra året och 10% det tredje året. Om du vill veta den genomsnittliga avkastningen kan du inte använda det aritmetiska genomsnittet. Varför? För när du hittar avkastning multiplicerar du, inte lägger till. Till exempel, det första året du multiplicerar med 1,05.,

  4. aritmetiskt geometriskt medelvärde

    detta används främst i kalkyl och maskinberäkning (dvs. som grund för många datorberäkningar). Det är relaterat till omkretsen av en ellips. När den först utvecklades av Gauss användes den för att beräkna planetariska banor. Den aritmetiska geometriska är (inte överraskande!) en blandning av aritmetiska och geometriska medelvärden. Matematiken är ganska komplicerad men du kan hitta en relativt enkel förklaring av matematiken här.,

  5. Root-Mean Square

    det är mycket användbart inom områden som studerar sinusvågor, som elektroteknik. Denna speciella typ kallas också det kvadratiska genomsnittet. Se: Kvadratisk Medelvärde / Rot Medelvärde Kvadrat.

  6. Heronian Mean

    används i geometri för att hitta volymen av en pyramidal frustum. En pyramidal frustum är i grunden en pyramid med spetsen skivad av.

  7. grafiskt medelvärde

    ett annat namn för lutningen på den sekanta linjen: motsvarande den genomsnittliga förändringstakten mellan två punkter.,

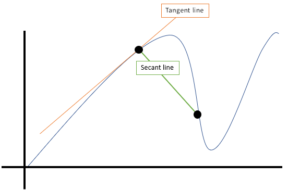
Vad är läget?

läget är det vanligaste numret i en uppsättning. Till exempel är läget i denna uppsättning siffror 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33

Vad är medianen?

medianen är mittnumret i en datamängd. För att hitta medianen, lista dina datapunkter i stigande ordning och hitta sedan mittnumret., Mittnumret i denna uppsättning är 28 eftersom det finns 4 nummer under det och 4 nummer ovan:
23, 24, 26, 26, 28, 29, 30, 31, 33

hur man hittar medelvärdet, medianen och läget för hand: steg

hur man hittar medelvärdet, medianen och läget: läge

hur man hittar medelvärdet, medianen och läget: medelvärdet

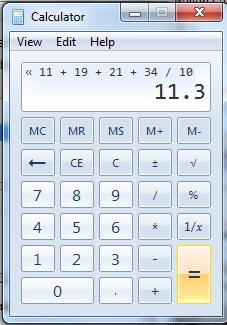
dela summan med antalet objekt för att hitta medelvärdet.

hur man hittar medelvärdet, medianen och läget: MEDIAN

om du hade ett udda tal i steg 3, Gå till steg 5. Om du hade ett jämnt nummer, gå till steg 6.,

Tips: Du kan ha mer än ett läge. Till exempel, läget för 1, 1, 5, 5, 6, 6 är 1, 5 och 6.

gilla förklaringen? Kolla in handboken praktiskt fusk statistik, som har hundratals fler steg-för-steg-lösningar, precis som den här!

SPSS Mean mode median

för att hitta SPSS mean mode median, måste du använda fliken frekvens. Det verkar lite kontraintuitivt, men fliken beskrivande statistik ger dig inte möjlighet att hitta läget eller medianen.,

SPSS har ett mycket liknande gränssnitt till Microsoft Excel. Därför, om du har använt Microsoft Excel tidigare, kommer du snabbt anpassa sig till SPSS.

SPSS Mean Mode Median: steg

titta på videon eller läs stegen nedan:

vänligen acceptera statistik, marknadsföringscookies för att titta på den här videon.

prov fråga: Hitta SPSS medelläge median för följande datamängd: 20,23,35,66,55,66

Steg 1: Öppna SPSS. I ” vad skulle du vilja göra?”dialogruta, klicka på” skriv in data ” radioknappen och klicka sedan på ”OK.”Ett nytt kalkylblad öppnas., Obs! Om du har valt ut den första hjälpskärmen kanske du inte ser det här alternativet. I så fall, börja bara vid steg 2.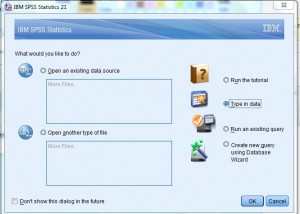

steg 2: Skriv in dina data i kalkylbladet. Du kan skriva in data i en kolumn eller flera kolumner om du har flera datauppsättningar. För detta exempel, skriv 20, 23, 35, 66, 55, 66 i kolumn 1. Lämna inte mellanslag mellan data (dvs. lämna inga tomma rader).

steg 2: Klicka på ”Analysera”, håll muspekaren över ”beskrivande statistik” och klicka sedan på ”frekvenser”.,”

steg 3: Klicka på” statistik ”och markera sedan rutorna” medel”,” läge ”och” median.”Klicka på” Fortsätt ”två gånger (välj ”ingen” som diagramtypen i det andra fönstret).
Obs! i vissa versioner av SPSS kanske du bara behöver klicka på” Fortsätt ” en gång och det kanske inte ger dig ett alternativ för diagramtyp.

frekvensresultaten visas som utdata. Den övre delen av utmatningen visar medelvärdet, läget och medianen.

om du bläddrar ner visar frekvenstabellen också läget., Läget definieras i statistiken som antalet med den högsta frekvensen (för denna provdatauppsättning är numret som visas mest 66, med två resultat i frekvenskolumnen).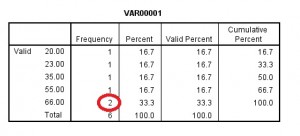

TI 83 medelvärde, medianvärde och läge

att hitta TI 83 medelvärde eller TI 83 median från en lista med data kan åstadkommas på två sätt: genom att ange en lista med data, eller genom att använda startskärmen för att skriva in kommandona., Att använda listfunktionen är lika enkelt som att skriva in data på startskärmen, och det har den extra fördelen att du kan använda data för andra ändamål efter att du har beräknat ditt medelvärde, läge och median (till exempel kanske du vill skapa ett TI 83 histogram).

steg för medelvärdet, medianen och läget på TI 83

titta på videon för medelvärdet och medianen eller läs stegen nedan (för läget, se den här noten):

vänligen acceptera statistik, marknadsföringscookies för att titta på den här videon.

Steg 1: Ange ovanstående data i en lista., Tryck på STAT-knappen och tryck sedan på ENTER. Ange det första numret (1250) och tryck sedan på ENTER. Fortsätt mata in nummer genom att trycka på ENTER-knappen efter varje inmatning.

steg 2: Tryck på STAT-knappen.

steg 3: Tryck på högerpilen för att markera ”Calc.”

steg 4: Tryck på ENTER för att välja” 1-Var Stats ” och skriv sedan in listnamnet. Till exempel, för att ange L1 tryck och .

Steg 5: Tryck på ENTER igen. Räknaren kommer att returnera medelvärdet, x. För denna datalista är TI 83-medelvärdet 884,05 fot (avrundat till 3 decimaler).

steg 6: pil ner tills du ser ”med.,”Detta är TI 83 median; för ovanstående data är medianen 813.05 Fötter.

Obs: TI-83 plus har ingen inbyggd funktion, men när du har angett din lista är det ganska lätt att upptäcka läget: det är bara det nummer som oftast förekommer i uppsättningen. Inte säker? Läs mer om läget här.

det är det!

förlorade din guidebok? Ladda ner en ny här på TI: s webbplats.

——————————————————————————

behöver du hjälp med en läxa eller testfråga?, Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert på området. Din första 30 minuter med en Chegg handledare är gratis!