män. Jag känner på något sätt att jag gillar det du säger.
Soc. Och jag, Meno, som det jag säger.
Från platos Meno
längden på diagonalen på enhetstorget är lika med kvadratroten av 2.
längden på diagonalen på enhetens kvadrat är lika med √2. Det här är inte riktigt bra nyheter. Var och en som någonsin kom över Pythagoras sats är medveten om faktumet., I den isosceles högra triangeln med benen av Längd 1 är hypotenusen, enligt Pythagoras sats – 12 + 12 = (hypotenus)2 – verkligen av längd √2. Motivationen för den här sidan är inte så mycket det faktum själv, men sättet att visa det utan att använda den berömda teoremet. Det kan faktiskt hävdas att Pythagoras sats kan ha blivit överanvänd, se ett nyfiken exempel.
ett argument som går tillbaka till figuren som dragits av Sokrates i platos Meno kan ha varit känt för Pythagoras själv, även om den senare bodde ett sekel tidigare.,
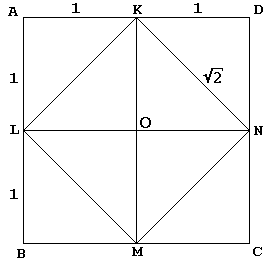
i dialogrutan leder Sokrates på sitt vanliga sätt en ung slav till en konstruktion av en kvadrat två gånger området för den givna:
den givna torget KLMN med centrum O skärs först av dess diagonaler i 4 lika trianglar. Sokrates bäddar KLMN i en större fyrkantig ABCD som om de reflekterar dessa trianglar var och en i sin hypotenus. Slaven medger då – och vem skulle inte? – torget är dubbelt så stort som square KLMN.
Sanningen ska fram, Sokrates ’ square ABCD mätt 4 på sidan, så att torget KLMN hade en yta på 8., Det är uppenbart att när vi börjar med kvadraten ABCD av sidan 2 (och därmed av området 4), kvadrat KLMN kommer att ha en yta på 2.
nu, i allmänhet, för ett positivt tal A, √A definieras som ett tal vars kvadrat är a:
(√a) 2.
å andra sidan vet varje elev av områden, att området på en kvadrat av sida B är lika med b2. Det följer då att sidan av en kvadrat med område A är exakt √A. Vi drar slutsatsen att sidan av torget KLMN är lika med √2. För en,
KN = √A.
den centrala punkten i argumentet är det faktum att KN i diagrammet spelar en dubbel roll., Förutom att vara en av sidorna av torget KLMN, det fungerar också som en diagonal av kvadrat OKDN. Det senare är naturligtvis en enhet kvadrat, vilket bevisar Vårt påstående.
(från ett lite annorlunda perspektiv nämns samma episod någon annanstans.)
















Lämna ett svar