visa Mobilmeddelande Visa alla anteckningar Dölj alla anteckningar

Mobilmeddelande
du verkar vara på en enhet med en ”smal” skärmbredd (dvs. du är förmodligen på en mobiltelefon). På grund av matematikens natur på denna sida är det bäst att se i landskapsläge. Om enheten inte är i liggande läge Många av ekvationerna kommer att köras utanför sidan av enheten (bör kunna rulla för att se dem) och några av menyalternativen kommer att avskuras på grund av den smala skärmbredden.,

avsnitt 4-11 : linjära approximationer

i det här avsnittet kommer vi att ta en titt på en applikation inte av derivat utan av tangentlinjen till en funktion. Naturligtvis, för att få tangentlinjen behöver vi ta derivat, så på något sätt är detta också en tillämpning av derivat.

\

ta en titt på följande diagram över en funktion och dess tangent linje.

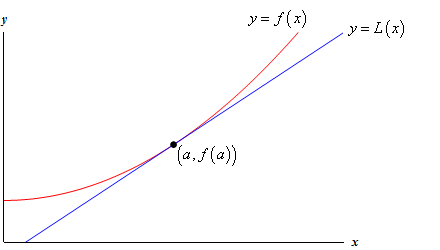
varför skulle vi göra det här? Låt oss ta en titt på ett exempel.,

linjära approximationer gör ett mycket bra jobb med att approximera värden på \(f\left( x \right)\) så länge vi stannar ”nära” \(x = a\). Men ju längre bort från \(x = a\) vi får sämre approximation är sannolikt att vara. Det största problemet här är att hur nära vi behöver stanna till \(x = A\) för att få en bra approximation beror på både den funktion vi använder och värdet på \(x = A\) som vi använder. Det kommer också ofta inte att finnas något enkelt sätt att förutsäga hur långt bort från \(x = a\) vi kan få och fortfarande ha en ”bra” approximation.,

Låt oss ta en titt på ett annat exempel som faktiskt används ganska tungt på vissa ställen.

detta är faktiskt en något viktig linjär approximation. I optik används denna linjära approximation ofta för att förenkla formlerna. Denna linjära approximation används också för att beskriva rörelsen av en pendel och vibrationer i en sträng.