Triangle Figure Angle-Side-Angle (Asa)
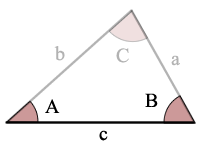
a = angle a
b = angle b
C = angle C
a = side a
b = side b
C = side C
p = perimeter
s = semi-perimeter
k = area
r = radie av inskriven cirkel
r = radie av avgränsad cirkel
kalkylator användning
varje beräkningsalternativ, som visas nedan, har underkulor som listar sekvensen av metoder som används i denna kalkylator för att lösa för okända vinkel-och sidvärden inklusive summan av vinklar i en triangel, lagen om Sines och lagen om cosinus., Det här är inte de enda sekvenserna du kan använda för att lösa dessa typer av problem.
- se även dessa Trigonometri räknare:
- lagen om Cosines Calculator
- lagen om Sines Calculator
lösa Triangle Theorems
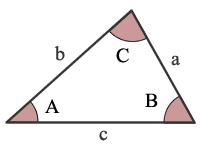
AAA är Vinkel, Vinkel, Vinkel
Ange de tre vinklar av en triangel identifierar inte unikt en triangel. Därför kan du bara beräkna den tredje vinkeln genom att ange två vinklar av en tringle.,
Med tanke på storleken på 2 vinklar av en triangel kan du beräkna storleken på den tredje vinkeln. Summan kommer att motsvara 180 ° eller π radianer.
C = 180° – A – B (i grader)
c = π – A – B (i radianer)
AAS är Vinkel, Vinkel, sida
Med tanke på storleken på 2 vinklar och 1 sida motsatt en av de givna vinklarna kan du beräkna storlekarna på de återstående 1-vinkeln och 2-sidorna.
använd Sum of Angles-regeln för att hitta den andra vinkeln, sedan
använd lagen om Sines för att lösa för var och en av de andra två sidorna.,
ASA är vinkel, sida, vinkel
Med tanke på storleken på 2 vinklar och storleken på den sida som ligger mellan de 2 vinklarna kan du beräkna storlekarna på de återstående 1-vinkeln och 2-sidorna.
använd Sum of Angles-regeln för att hitta den andra vinkeln, sedan
använd lagen om Sines för att lösa för var och en av de andra två sidorna.,
ASS (eller SSA) är vinkel, sida, sida
Med tanke på storleken på 2 sidor (A och C där en< C) och storleken på vinkeln A som inte ligger mellan dessa 2 sidor kan du kanske beräkna storleken på den återstående 1-sidan och 2-vinklarna, beroende på följande villkor.,f cosinus för att lösa för var och en av de andra två vinklarna
presentera 2 fulla lösningar
exempel: 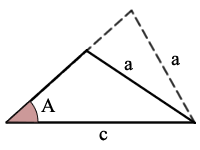
sin(a) = a/c, det finns en möjlig triangel
använd lagen om Sines för att lösa för en vinkel, C
använd summan av vinklarna för att hitta den andra vinkeln, B
använd lagen om Sines för att lösa för den sista sidan, b
exempel: 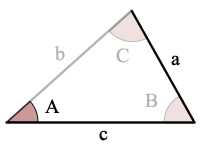
sin(a) > a/c, det finns inga möjliga trianglar
felmeddelande: sin(a) > a/C så det finns inga lösningar och ingen triangel!,
exempel: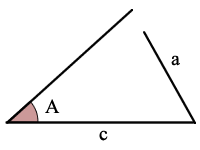
SAS är sida, vinkel, sida
Med tanke på storleken på 2 sidor (C och a) och storleken på vinkeln B som ligger mellan dessa 2 sidor kan du beräkna storleken på den återstående 1-sidan och 2-vinklarna.
använd Cosinuslagen för att lösa för den återstående sidan, b
bestäm vilken sida, A eller c, som är minsta och använd lagen om Sines för att lösa för storleken på motsatt vinkel, A respektive C.,
använd sum of Angles Rule för att hitta den sista vinkeln
SSS är sida, sida, sida
Med tanke på storlekarna på de 3 sidorna kan du beräkna storlekarna på alla 3 vinklar i triangeln.
använd Cosinuslagen för att lösa för vinklarna. Du kan också använda summan av vinklar regeln att hitta den slutliga vinkeln när du vet 2 av dem.,sin-1
cosinus lag
Om A, B och c är längderna på benen i en triangel motsatt vinklarna A, B respektive C; då står cosinuslagen:
a2 = C2 + b2 – 2BC cos A, löser för cos a, cos A = ( b2 + c2 – a2 ) / 2BC
b2 = a2 + c2 – 2CA cos b, löser för cos b = ( c2 + a2 – b2 ) / 2CA
C2 = B2 + A2 – 2AB Cos C, lösa för Cos C, Cos c = ( a2 + b2 – c2 ) / 2AB
lösa, till exempel, för en vinkel, a = cos-1
andra triangle egenskaper
triangle omkrets, p = a + b + c
triangle semi-Perimeter, s = 0.,5 * (a + b + c)
Triangelområde, k = √
radie av inskriven cirkel i triangeln, r = √
radie av avgränsad cirkel runt triangel, R = (abc) / (4K)
referenser/ Ytterligare läsning
Weisstein, Eric W. ”ASS teorem.”Från MathWorld– En Wolfram Webbresurs. ASS Sats.
matematik är kul-lösa SAS trianglar
















Lämna ett svar