en vektor har magnitud (hur länge det är) och riktning:
här är två vektorer:

de kan multipliceras med ”Dot Product” (se även Cross Product).,
vi kan beräkna Dot-produkten av två vektorer på så sätt:

a · b = |a| × |b| × cos(θ)
var:
|a| är storleken (längden) av vektor a
|b| är storleken (längden) av vektor b
θ är vinkeln mellan en och B
så vi multiplicerar längden på en gånger längden på b, sedan multiplicera med cosinus av vinkeln mellan A och b
eller så kan vi beräkna det så här:
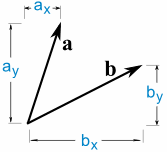
a · b = AX × BX + ay × by
så vi multiplicerar X: erna, multiplicerar y: erna, lägg sedan till.,
båda metoderna fungerar!
och resultatet är ett tal (kallas en ”skalär” så vi vet att det inte är en vektor).
Obs! Du kan använda Vektorkalkylenför att hjälpa dig.
Varför cos(θ) ?
OK, för att multiplicera två vektorer är det meningsfullt att multiplicera sina längder tillsammans men bara när de pekar i samma riktning.,
så vi gör en ”punkt i samma riktning” som den andra genom att multiplicera med cos(θ):
 |
 |
|
| vi tar komponenten i en som ligger bredvid b |
som att skina ett ljus för att se där skuggan ligger |
då multiplicerar vi !,
rät vinkel
När två vektorer är i rät vinkel mot varandra är punktprodukten noll.
detta kan vara ett praktiskt sätt att ta reda på om två vektorer är i rät vinkel.
tre eller fler dimensioner
allt detta fungerar också bra i 3 (eller fler) dimensioner.
och kan faktiskt vara mycket användbart!
Jag försökte en beräkning som en gång, men arbetade allt i vinklar och avstånd … det var mycket svårt, involverade massor av trigonometri, och min hjärna skadade. Metoden ovan är mycket lättare.,
Cross Product
Dot-produkten ger ett skalärt (vanligt nummer) svar och kallas ibland scalar-produkten.
men det finns också Korsprodukten som ger en vektor som svar, och kallas ibland vektorprodukten.

















Lämna ett svar