Visa mobil meddelande Visa alla anteckningar Dölj alla anteckningar
avsnitt 3-1 : parametriska ekvationer och kurvor
till denna punkt (i både kalkyl I och kalkyl II) har vi tittat nästan uteslutande på funktioner i formen \(y = f\left( x \right)\) eller \(x = H\left( y \right)\) och nästan alla formler som vi har utvecklat kräver att funktionerna är i en av dessa två former. Problemet är att inte alla kurvor eller ekvationer som vi skulle vilja titta på faller lätt i denna form.
ta till exempel en cirkel. Det är lätt att skriva ner ekvationen för en cirkel centrerad vid ursprunget med radie \(r\).,
\
Vi kommer dock aldrig att kunna skriva ekvationen för en cirkel ner som en enda ekvation i någon av ovanstående former. Visst kan vi lösa för \(x\) eller \(y\) som följande två formler visar
\
men det finns faktiskt två funktioner i var och en av dessa. Varje formel ger en del av cirkeln.
\
tyvärr arbetar vi vanligtvis på hela cirkeln, eller kan helt enkelt inte säga att vi bara kommer att arbeta på en del av den. Även om vi kan begränsa saker till bara en av dessa delar är funktionen fortfarande ofta ganska obehaglig att arbeta med.,
\
denna tredje variabel betecknas vanligtvis av \(T\) (som vi gjorde här) men behöver inte vara självklart. Ibland kommer vi att begränsa värdena på \(t\) som vi kommer att använda och vid andra tillfällen kommer vi inte. detta kommer ofta att vara beroende av problemet och precis vad vi försöker göra.
för att visualisera precis vad en parametrisk kurva är låtsas att vi har en stor tank med vatten som är i ständig rörelse och vi släpper en ping pong boll i tanken., Punkten \(\left ({x,y} \right) = \left ({f \left( t\right),g \left(t \right)}\ right)\) representerar sedan platsen för ping pong-bollen i tanken vid tiden\ (t\) och den parametriska kurvan kommer att vara ett spår av alla platser i ping pong-bollen. Observera att detta inte alltid är en korrekt analogi men det är användbart att hjälpa till att visualisera precis vad en parametrisk kurva är.
skissa en parametrisk kurva är inte alltid en lätt sak att göra. Låt oss ta en titt på ett exempel för att se ett sätt att skissa en parametrisk kurva., Detta exempel kommer också att illustrera varför denna metod vanligtvis inte är bäst.
vid denna tidpunkt är vårt enda alternativ för att skissa en parametrisk kurva att välja värden på\ (t\), koppla in dem i parametriska ekvationer och sedan rita punkterna. Så, låt oss koppla in några \(T\) s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Tyvärr finns det inget riktigt svar på denna fråga vid denna tidpunkt. Vi väljer helt enkelt \(T\) tills vi är ganska övertygade om att vi har en bra uppfattning om hur kurvan ser ut. Det är detta problem med att välja ” bra ” värden på \(t\) som gör denna metod för att skissa parametriska kurvor till ett av de fattigare valen. Ibland har vi inget val, men om vi har ett val bör vi undvika det.
vi diskuterar en alternativ grafmetod i senare exempel som hjälper till att förklara hur dessa värden för \(t\) valdes.,
Vi har ytterligare en idé att diskutera innan vi faktiskt skissar kurvan. Parametriska kurvor har en rörelseriktning. Rörelseriktningen ges genom att öka \(t\). Så, när vi plottar parametriska kurvor, inkluderar vi också pilar som visar rörelseriktningen. Vi kommer ofta att ge värdet av \(T\) som gav specifika punkter på grafen samt att göra det klart värdet av \(T\) som gav den punkten.
här är skissen av denna parametriska kurva.
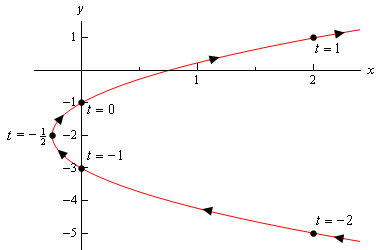
så det ser ut som om vi har en parabola som öppnas till höger.,
innan vi avslutar detta exempel finns det en något viktig och subtil punkt som vi måste diskutera först. Observera att vi såg till att inkludera en del av skissen till höger om punkterna som motsvarar \(T = – 2\) och \(T = 1\) för att indikera att det finns delar av skissen där. Hade vi helt enkelt stoppat skissen på dessa punkter indikerar vi att det inte fanns någon del av kurvan till höger om dessa punkter och det kommer tydligt att vara. Vi har bara inte beräknat några av dessa punkter.,
detta kan verka som en obetydlig punkt, men som vi ser i nästa exempel är det viktigare än vi kanske tror.
innan du tar itu med ett mycket enklare sätt att skissa den här grafen låt oss först ta itu med frågan om gränser för parametern. I föregående exempel hade vi inga gränser för parametern. Utan gränser för parametern fortsätter grafen i båda riktningarna som visas i skissen ovan.
Vi kommer ofta att ha gränser för parametern men detta kommer att påverka skissen av parametriska ekvationer., För att se denna effekt låt oss se en liten variation av föregående exempel.
Observera att den enda skillnaden här är förekomsten av gränserna för\(t\). Alla dessa gränser gör är att berätta för oss att vi inte kan ta något värde av \(t\) utanför detta intervall. Därför kommer den parametriska kurvan endast att vara en del av kurvan ovan. Här är den parametriska kurvan för detta exempel.,
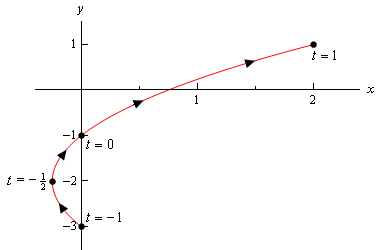
Observera att med denna skiss började vi och stoppade skissen direkt på punkterna som härrör från slutpunkterna i intervallet \(t\) s. kontrast detta med skissen i föregående exempel där vi hade en del av skissen till höger om ”start” och ”end” punkter som vi beräknade.
i det här fallet börjar kurvan vid \(t = – 1\) och slutar vid \(t = 1\), medan kurvan i föregående exempel inte riktigt började vid rätt mest punkter som vi beräknade., Vi måste vara tydliga i våra skisser om kurvan börjar/slutar rätt vid en punkt, eller om den punkten helt enkelt var den första/sista som vi beräknade.
det är nu dags att ta en titt på en enklare metod för att skissa denna parametriska kurva. Denna metod använder det faktum att vi i många, men inte alla, fall faktiskt kan eliminera parametern från parametriska ekvationer och få en funktion som endast involverar \(x\) och \(y\). Vi kommer ibland att kalla detta den algebraiska ekvationen för att skilja den från de ursprungliga parametriska ekvationerna., Det kommer att finnas två små problem med den här metoden, men det blir lätt att ta itu med dessa problem. Det är dock viktigt att notera att vi inte alltid kommer att kunna göra detta.
hur vi eliminerar parametern beror på de parametriska ekvationer som vi har. Låt oss se hur man eliminerar parametern för uppsättningen parametriska ekvationer som vi har arbetat med till denna punkt.
att få en skiss av parametrisk kurva när vi har eliminerat parametern verkar ganska enkelt. Allt vi behöver göra är att gravera ekvationen som vi hittade genom att eliminera parametern., Som redan nämnts finns det dock två små problem med denna metod. Den första är rörelseriktningen. Ekvationen som endast involverar \(x\) och\ (y\) ger inte rörelseriktningen för den parametriska kurvan. Detta är i allmänhet ett enkelt problem att åtgärda dock. Låt oss ta en snabb titt på derivaten av parametriska ekvationer från det sista exemplet. De är,
\
Observera att derivatet \(x\) inte är lika användbart för denna analys eftersom det kommer att vara både positivt och negativt och därmed kommer \(x\) att både öka och minska beroende på värdet av \(t\)., Det hjälper inte med riktning mycket som följer kurvan i båda riktningarna kommer att uppvisa både ökande och minskande \(x\).
i vissa fall kommer endast en av ekvationerna, som det här exemplet, att ge riktningen medan i andra fall endera kan användas. Det är också möjligt att båda derivaten i vissa fall skulle behövas för att bestämma riktningen. Det kommer alltid att vara beroende av den individuella uppsättningen parametriska ekvationer.,
det andra problemet med att eliminera parametern illustreras bäst i ett exempel eftersom vi kommer att köra in i detta problem i de återstående exemplen.
okej, det var ett riktigt långt exempel. De flesta av dessa typer av problem är inte så länge. Vi hade bara mycket att diskutera i den här så att vi kunde få ett par viktiga idéer ur vägen. Resten av exemplen i det här avsnittet bör inte ta så lång tid att gå igenom.
låt oss nu ta en titt på ett annat exempel som illustrerar en viktig idé om parametriska ekvationer.,
Så vi såg i de två sista exemplen två uppsättningar parametriska ekvationer som på något sätt gav samma graf. Men eftersom de spårade grafen ett annat antal gånger måste vi verkligen tänka på dem som olika parametriska kurvor åtminstone på något sätt. Detta kan verka som en skillnad som vi inte behöver oroa sig för, men som vi kommer att se i senare avsnitt kan detta vara en mycket viktig skillnad. I några av de senare avsnitten kommer vi att behöva en kurva som spåras ut exakt en gång.,
innan vi går vidare till andra problem låt oss kortfattat erkänna vad som händer genom att ändra \(T\) till en nt i dessa typer av parametriska ekvationer. När vi har att göra med parametriska ekvationer som endast omfattar sines och cosines och de båda har samma argument om vi ändrar argumentet från \(T\) till nt ändrar vi helt enkelt hastigheten med vilken kurvan spåras ut. If\ (n > 1\) Vi kommer att öka hastigheten och om\ (n < 1\) Vi kommer att minska hastigheten.
Låt oss ta en titt på ett par fler exempel.,
till denna punkt har vi sett exempel som skulle spåra den fullständiga grafen som vi fick genom att eliminera parametern om vi tog ett tillräckligt stort utbud av \(T\) s. men i föregående exempel har vi nu sett att detta inte alltid kommer att vara fallet. Det är mer än möjligt att ha en uppsättning parametriska ekvationer som kontinuerligt kommer att spåra ut bara en del av kurvan. Vi kan vanligtvis avgöra om detta kommer att hända genom att leta efter gränser för \(x\) och \(y\) som åläggs oss av parametrisk ekvation.,
Vi kommer ofta att använda parametriska ekvationer för att beskriva sökvägen för ett objekt eller en partikel. Låt oss ta en titt på ett exempel på det.
Vi bör ge en liten varning vid denna tidpunkt. På grund av de idéer som är involverade i dem koncentrerade vi oss på parametriska kurvor som retracerade delar av kurvan mer än en gång. Men bli inte för låst i tanken att detta alltid kommer att hända. Många, om inte de flesta parametriska kurvor kommer bara att spåra ut en gång. Det första vi tittade på är ett bra exempel på detta. Den parametriska kurvan kommer aldrig att upprepa någon del av sig själv.,
det finns ett sista ämne som ska diskuteras i det här avsnittet innan du går vidare. Hittills har vi börjat med parametriska ekvationer och eliminerat parametern för att bestämma parametrisk kurva.
det finns dock tillfällen då vi vill gå åt andra hållet. Med tanke på en funktion eller ekvation kanske vi vill skriva ner en uppsättning parametriska ekvationer för den. I dessa fall säger vi att vi parametrerar funktionen.
om vi tar Exempel 4 och 5 som exempel kan vi göra detta för ellipser (och därmed cirklar)., Med tanke på ellipsen
\
en uppsättning parametriska ekvationer för det skulle vara,
\
denna uppsättning parametriska ekvationer kommer att spåra ellipsen från punkten \(\left ({a,0}\ right)\) och kommer att spåra i moturs riktning och kommer att spåra exakt en gång i intervallet \(0 \ le t \le 2 \ pi\). Detta är en ganska viktig uppsättning parametriska ekvationer som det används kontinuerligt i vissa ämnen med att hantera ellipser och / eller cirklar.
varje kurva kan parametreras på mer än ett sätt. Något av följande kommer också att parametrisera samma ellips.,
\
närvaron av \(\omega \) kommer att ändra den hastighet som ellipsen roterar som vi såg i Exempel 5. Observera också att de två sista kommer att spåra ellipser medurs (du kanske vill verifiera detta). Observera också att de inte alla börjar på samma plats(om vi tänker på \(t = 0\) som utgångspunkt som är).
det finns många fler parametriseringar av en ellips naturligtvis, men du får idén. Det är viktigt att komma ihåg att varje parameterisering kommer att spåra kurvan en gång med ett potentiellt annorlunda intervall av \(T\)’s., Varje parameterisering kan rotera med olika rörelseriktningar och kan börja på olika punkter.
Du kan upptäcka att du behöver en parametrisering av en ellips som börjar på en viss plats och har en viss rörelseriktning och så att du nu vet att med lite arbete kan du skriva ner en uppsättning parametriska ekvationer som ger dig beteendet som du är ute efter.
låt oss nu skriva ner ett par andra viktiga parameteriseringar och alla kommentarer om rörelseriktning, startpunkt och intervall av \(T\)’S för ett spår (om tillämpligt) är fortfarande sanna.,
först, eftersom en cirkel är inget annat än ett speciellt fall av en ellips kan vi använda parametriseringen av en ellips för att få parametriska ekvationer för en cirkel centrerad vid ursprunget till radie \(r\) också. Ett möjligt sätt att parametrisera en cirkel är,
\ \
vid denna tidpunkt kanske det inte verkar så användbart att göra en parameterisering av en funktion som denna, men det finns många fall där det faktiskt blir lättare, eller det kan till och med krävas, att arbeta med parameteriseringen istället för själva funktionen., Tyvärr förekommer nästan alla dessa fall i en Calculus III-kurs.
















Lämna ett svar