Vektorer er mye nyttig i vitenskap for å beskrive noe som har både en retning, så vel som en styrke. De er vanligvis trukket med hjelp av pekte pilene, lengden på som vil representere vector omfanget. En quarterback ‘ s pass er den enkle eksempel fordi den har retning vanligvis et sted downfield og en styrke. Noen ganger må vi håndtere to vektorer sammen arbeider på enkelte objekt. I slike tilfeller vinkler mellom disse vektorene er viktig., Dette emnet vil forklare vinkelen mellom to vektorer formel, så vel som eksempler. La oss lære det!
Konsept av Vektorer
Av feltet, vektorer kan brukes til å representere hvilket som helst antall av fysiske objekter eller aktiviteter. Eksempelvis. Vind, for eksempel, er en vektorstyrt kvantitet. Det er fordi på et gitt sted har en retning, så vel som styrke. Vi kan lage et kart av luftmengde på ethvert tidspunkt, og deretter, ved å tegne vind vektorer for en rekke ulike geografiske steder.
Mange egenskaper av objekter i bevegelse er også en form for vektorer., I billiard ball, sin fartsvektoren beskriver sin bevegelse. Det viser retningen på pilen vektor merker som retningen av bevegelse, og lengden av vektoren representerer hastigheten på ballen.
billiard ball er momentum er også et eksempel på vektorstyrt kvantitet. Så det er lik masse ganger hastighet. Derfor, momentum vektor av ballpoints i samme retning som sin fartsvektoren. Og momentum vektor omfanget vil være multiplikasjon produkt av ballens hastighet og dens masse.,
I forhold til matematikk, en vektor er en gjenstand som har en definerbar størrelse og retning. Som vektorer er ikke det samme som standard linjer eller former, vi trenger å bruke noen spesielle formler for å finne vinkler mellom dem.
Formelen for Vinkelen mellom To Vektorer
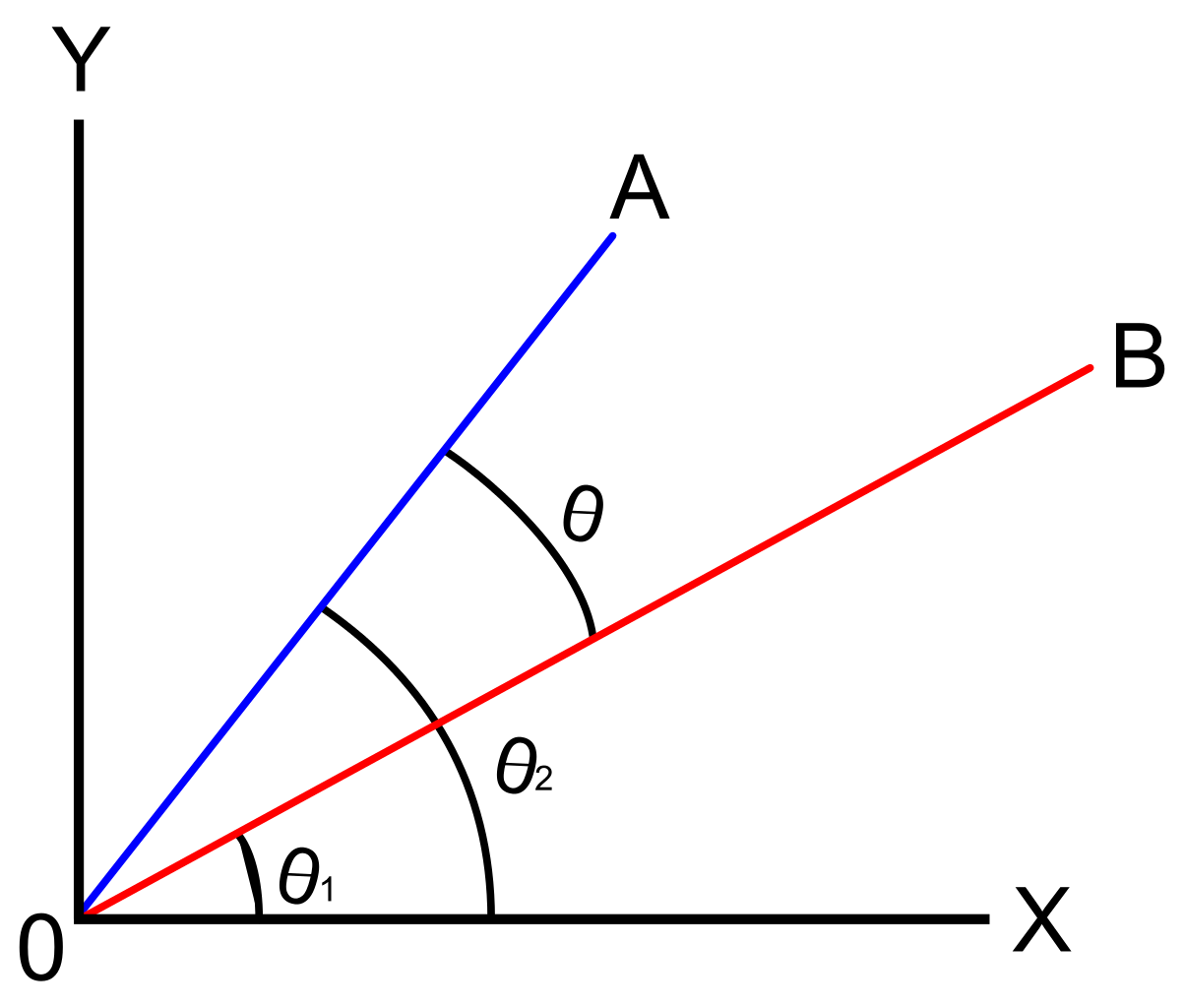
vinkelen mellom to vektorer vil være utsatt ved et enkelt punkt, som er kalt som den korteste vinkel som vi er nødt til å snu en av vektorene til posisjon av co-directional med en annen vektor.,
diskusjon om retning vinkler av vektorer fokuserer på å finne vinkelen av en vektor med hensyn til den positive x-aksen. Dette vil fokusere på vinkelen mellom to vektorer i standard posisjon. En vektor er sagt å være i standard posisjon hvis det første punktet er origo (0, 0).
Hvis de to vektorer er antatt som a og b så dot laget er definert som en .b. La oss anta at disse to vektorer er atskilt med vinkel \(\theta\). Å vite hva som er vinkelen måling som vi vil løse med hjelp av formelen gitt:
Vi kjenner dot produkt:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Nå, vinkelen mellom to vektorer formelen er:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\)
Hvor \\(theta\) er vinkelen mellom a og b vektorer.
Løst Eksempler for Vinkelen mellom To Vektorer Formel
Q. 1: Beregn vinkelen mellom to vektorer 3i + 4j – k og 2i – j + k.
Løsning: La,
a = 3i + 4j – k og
b = 2i – j + k
Vi definerer prikk-produktet som:
en .b = (3i + 4j – k).(2i – j + k)
















Legg igjen en kommentar