Sannsynligheten for kaster to terninger med den seks-kantede dotssuch som 1, 2, 3, 4, 5 og 6 prikker i hver dør.

Når to terninger blir kastet samtidig er dermed antall hendelse kan være 62 = 36 fordi hver dør har 1 til 6 antall på sine ansikter. Da de mulige utfallene er vist i tabellen nedenfor.,
Sannsynlighet – Eksempel plass for to terninger (utfall):
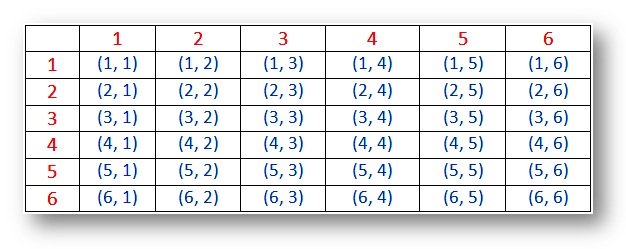
Merk:
(I) resultater (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) og (6, 6) kalles doublets.
(ii) par (1, 2) og (2, 1) er forskjellige utfall.
Arbeidet ut problemer som involverer sannsynlighet for kaster to terninger:
1. To terninger er rullet. La A, B, C være hendelser for å få en sum av 2, en sum av 3, og en sum av 4 henholdsvis., Deretter viser at
(i) Et er en enkel hendelse
(ii) B og C er sammensatte hendelser
(iii) A og B er gjensidig utelukkende
Løsning:
Klart, vi har
A = {(1, 1)}, B = {(1, 2), (2, 1)} og C = {(1, 3), (3, 1), (2, 2)}.
(jeg) Siden består av et enkelt eksempel punkt, det er en enkel hendelse.
(ii) Siden både B og C inneholder mer enn én prøve punkt, hver og en av dem er en sammensatt hendelse.
(iii) Siden A ∩ B = ∅, A og B er gjensidig utelukkende.
2. To terninger er rullet., En er tilfellet at summen av tallene som vises på de to terningene er 5, og B er tilfelle at minst en av terningene viser opp en 3.
Er det to hendelser (jeg) er gjensidig utelukkende, (ii) uttømmende? Gi argumenter til støtte for ditt svar.
Løsning:
Når to terninger er rullet, vi har n(S) = (6 × 6) = 36.
Nå, En = {(1, 4), (2, 3), (4, 1), (3, 2)}, og
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(jeg) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
Derfor, A og B er ikke gjensidig utelukkende.,
(ii) Også, A ∪ B ≠ S.
Derfor, A og B er ikke uttømmende hendelser.
Flere eksempler knyttet til spørsmål om sannsynligheter for å kaste to terninger.
3. To terningene er kastet samtidig.,) å få en dublett
(v) får en sum av 8
(vi) å få summen divideres med 5
(vii) å få summen av minst 11
(viii) å få et multiplum av 3 som summen
(ix) å få en total av minst 10
(x) for å få et partall som summen
(xi) å få et primtall som summen
(xii) å få en dublett av partall
(xiii) å få et multiplum av 2 på en dør og et multiplum av 3 på den andre dør
Løsning:
To forskjellige terningen er kastet samtidig som nummer 1, 2, 3, 4, 5 og 6 på deres ansikter., Vi vet at i en enkelt kastet av to forskjellige terninger, totalt antall mulige utfall er (6 × 6) = 36.
(jeg) får seks som et produkt:
La E1 = begivenhet for å få seks som et produkt. Antall hvis produktet er seks vil bli E1 = = 4
Derfor, sannsynlighet ofgetting «seks som et produkt’
Antall gunstige utfall
P(E1) = Totalt antall mulige utfall
= 4/36
= 1/9
(ii) å få summen ≤ 3:
La E2 = begivenhet for å få summen ≤ 3., Antall summen ≤ 3 vil være E2 = = 3
Derfor, sannsynlighet ofgetting ‘sum ≤ 3’
Antall gunstige utfall
P(E2) = Totalt antall mulige utfall
= 3/36
= 1/12
(iii) å få summen ≤ 10:
La E3 = begivenhet for å få summen ≤ 10. Antall summen ≤ 10 vil være E3 =
= 33
Derfor, sannsynlighet ofgetting ‘sum ≤ 10’
Antall gunstige utfall
P(E3) = Totalt antall mulige utfall
= 33/36
= 11/12
(iv)å få en dublett:La E4 = begivenhet for å få en dublett., Antall som dublett vil være E4 = = 6
Derfor, sannsynlighet ofgetting ‘en dublett’
Antall gunstige utfall
P(E4) = Totalt antall mulige utfall
= 6/36
= 1/6
(v)får en sum av 8:
La E5 = begivenhet for å få en sum av 8. Antallet som er en sum av 8 vil være E5 = = 5
Derfor, sannsynlighet ofgetting ‘en sum av 8’
Antall gunstige utfall
P(E5) = Totalt antall mulige utfall
= 5/36
(vi)å få summen divideres med 5:
La E6 = begivenhet for å få summen delelig med 5., Antall summen divideres med 5 vil bli E6 = = 7
Derfor, sannsynlighet ofgetting ‘sum delelig med 5’
Antall gunstige utfall
P(E6) = Totalt antall mulige utfall
= 7/36
(vii)å få summen av minst 11:
La E7 = begivenhet for å få summen av minst 11. Hendelsene summen av minst 11 vil bli E7 = = 3
Derfor, sannsynlighet ofgetting ‘summen av minst 11’
Antall gunstige utfall
P(E7) = Totalt antall mulige utfall
= 3/36
= 1/12
(viii) å få amultiple av 3 som summen:
La E8 = begivenhet for å få et multiplum av 3 som summen., Hendelsene i et multiplum av 3 som summen vil være E8 = = 12
Derfor, sannsynlighet ofgetting ‘et multiplum av 3 som summen’
Antall gunstige utfall
P(E8) = Totalt antall mulige utfall
= 12/36
= 1/3
(ix) å få en totalof atleast 10:
La E9 = begivenhet for å få en total av minst 10., Hendelser av en total av minst 10 vil være E9 = = 6
Derfor, sannsynlighet ofgetting ‘en total av minst 10’
Antall gunstige utfall
P(E9) = Totalt antall mulige utfall
= 6/36
= 1/6
(x) for å få en evennumber som summen:
La E10 = begivenhet for å få et partall som summen., Hendelsene i et partall som summen vil være E10 = = 18
Derfor, sannsynlighet ofgetting ‘et partall som summen
Antall gunstige utfall
P(E10) = Totalt antall mulige utfall
= 18/36
= 1/2
(xi) å få en primenumber som summen:
La E11 = begivenhet for å få et primtall som er summen., Hendelsene i et primtall som summen vil være E11 = = 15
Derfor, sannsynlighet ofgetting ‘et primtall som summen’
Antall gunstige utfall
P(E11) = Totalt antall mulige utfall
= 15/36
= 5/12
(xii) komme adoublet av partall:
La E12 = begivenhet for å få en dublett av partall., Hendelsene i en dublett av partall vil være E12 = = 3
Derfor, sannsynlighet ofgetting ‘en dublett av partall’
Antall gunstige utfall
P(E12) = Totalt antall mulige utfall
= 3/36
= 1/12
(xiii) komme amultiple av 2 på en dør og et multiplum av 3 på den andre dør:
La E13 = begivenhet for å få et multiplum av 2 på en dør og et multiplum av 3 på den andre dør., Hendelsene i et multiplum av 2 på en dør og et multiplum av 3 på den andre dør vil være E13 = = 11
Derfor, sannsynlighet ofgetting ‘et multiplum av 2 på en dør og et multiplum av 3 på den andre dør’
Antall gunstige utfall
P(E13) = Totalt antall mulige utfall
= 11/36
4. Twodice er kastet. Finn (jeg) oddsen i favør av å få summen 5, og (ii) theodds mot å få summen 6.
Løsning:
Vi vet at i en enkelt kastet av to die, totalt numberof mulig utfall er (6 × 6) = 36.
La S være eksempel på plass. Deretter,n(S) = 36.,
(jeg) oddsen i favør av å få summen 5:
La E1 være tilfelle for å få summen 5. Så,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Derfor, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ oddsen i favør av E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) odds mot å få summen 6:
La E2 være tilfelle for å få summen 6. Så,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Derfor, P(E2) = n(E2)/n(S) = 5/36
⇒ odds mot E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., To terninger, en blå og en orange, er rullet samtidig. Finn sannsynligheten for å få
(jeg), tilsvarende tall på begge
(ii) to tallene som vises på dem, summen er 9.,
Løsning:
De mulige utfallene er
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
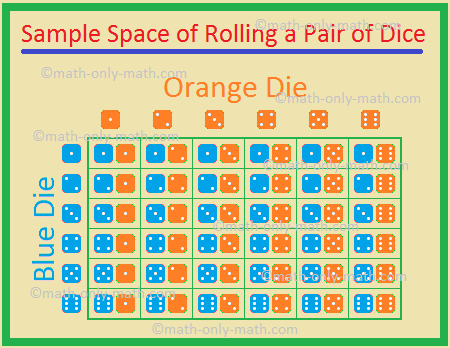
Derfor, totalt antall mulige utfall = 36.,
(jeg) Antall gunstige utfall for hendelsen E
= antall utfall etter å ha like mange på begge terningene
= 6 .
Så, per definisjon, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Antall gunstige utfall for arrangementet F
= Antall utfall i hvilke to tall som vises på dem har summen 9
= 4 .
Derfor, per definisjon, P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
Disse eksemplene vil helpus for å løse forskjellige typer problemer basert på sannsynlighet for rollingtwo terninger.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Legg igjen en kommentar