Prismer (Norsk)

Gå til Areal eller Volum.

Et prisme er et solid objekt med:

Et tverrsnitt er formen laget ved å kutte rett over et objekt.

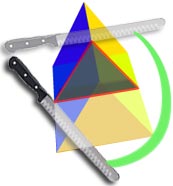
tverrsnitt av dette objektet er en trekant …

.. den har samme tverrsnitt langs dens lengde …

… så det er en trekantet prisme.,

Prøve å tegne en figur på et stykke papir (ved hjelp av rette linjer) Så tenk det strekker seg opp fra arket … … det er et prisme !

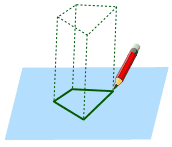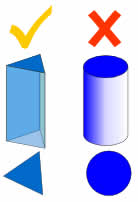
Ingen Kurver!

Et prisme er en polyhedron, noe som betyr at alle ansikter er flate!

For eksempel, en sylinder er ikke et prisme, fordi det har buede kanter.,

Baser

endene av et prisme er parallell
og hver og en er kalt en base.

Sider

Den siden som vender mot av et prisme er parallelograms
(4-kantede figurer med motstående sider parallelle)

Dette er alle Prismer:

og mer!

Vanlig vs Uregelmessig Prismer

Alle de tidligere eksemplene er Vanlig Prismer, fordi tverrsnittet er vanlig (med andre ord er det en figur med like kanten lengder, og like vinkler.,)

Here is an example of an Irregular Prism:

Irregular Pentagonal Prism:
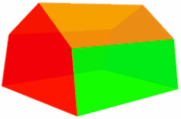		Cross-Section
It is «irregular» because the cross-section is not «regular» in shape.,div> Areal = 2 × Base-Området + Base Omkretsen × Lengde Eksempel: Hva er arealet av et prisme der basen området er 25 m2, basen omkretsen er 24 m, og lengden er 12 m: Areal = 2 × Base-Området + Base Omkretsen × Lengde = 2 × 25 m2 + 24 m x 12 m = 50 m2 + 288 m2 = 338 m2 (Merk: vi har et Område Beregning Verktøy) Volumet av et Prisme Volumet av et prisme er et område i den ene enden ganger lengden av prismet., Volum = Base-Området × Lengde Eksempel: Hva er volumet av et prisme der basen området er 25 m2 og som er 12 meter lang: Volum = Areal × Lengde = 25 m2 × 12 m = 300 m3 Leke med det her., Formelen fungerer også når det «lener seg over» (skrå) men husk at høyden er i rett vinkel til base: Og dette er grunnen: stabel kan lene seg over, men fortsatt har den samme volum Articles Legg igjen en kommentar Avbryt svar Din e-postadresse vil ikke bli publisert. Obligatoriske felt er merket med * Kommentar Navn * E-post * Nettsted Lagre mitt navn, e-post og nettside i denne nettleseren for neste gang jeg kommenterer. Deutsch Nederlands Svenska Norsk Dansk Español Français Português Italiano Română Polski Čeština Magyar Suomi 日本語 한국어 © 2021 Tombouctou Tema av Anders Norén — Opp ↑