Når Vinklene i en Trekant ikke Legge opp til 180 Grader

1. Innledning

Gjør vinklene i en trekant legge opp til 180 grader eller $\pi$ radianer? Svaret er «noen ganger ja, andre ganger nei’. Er dette et viktig spørsmål? Ja, fordi det fører til en forståelse av at det er ulike geometrier basert på ulike aksiomer eller «regler for spillet av geometri’. Er det en meningsfylt spørsmål? Vel nei, i hvert fall ikke før vi har blitt enige om betydningen av ordene «vinkel» og’triangle’, ikke før vi kjenner reglene for spillet., I denne artikkelen vil vi kort diskutere den underliggende aksiomene og gi en enkel bevis på at summen av vinklene i en trekant på overflaten av en enhet sfæren er ikke lik $\pi$ men $\pi$ pluss arealet av trekanten. Vi skal bruke det faktum at arealet av overflaten til en enhet sfære er $4\pi$.

2. Den Store Teorem

Før vi kan si hva en trekant er at vi må bli enige om hva vi mener med punkter og linjer. Vi jobber med sfærisk geometri (bokstavelig talt geometri på overflaten av en kule)., I dette geometri plassen er overflaten av sfære; de poeng er poeng på overflaten, og linjen av korteste avstanden mellom to punkter er den store sirkel som inneholder to poeng. En stor sirkel (likethe Ekvator) kutt sfæren i to like halvdeler. Denne geometrien har åpenbare programmer for å avstander mellom steder og air-ruter på Jorden.,

Roterende kule viser stor sirkel

vinkelen mellom to store sirkler på et punkt P er Euclidean vinkelen mellom retningene av sirkler (eller strengt mellom tangenter til sirkler på P). Dette presenterer ingen problemer med navigering på Jorden fordi på et gitt tidspunkt tror vi at vinkelen mellom to retningene som om Jorden var flat på det tidspunktet.

En lune er en del av overflaten av det området som er avgrenset av to store sirkler som møtes på antipodal poeng., Vi først se på det området av en lune og deretter introdusere en annen stor sirkel som deler her inn i trekanter.

Roterende kule viser 4 lunes

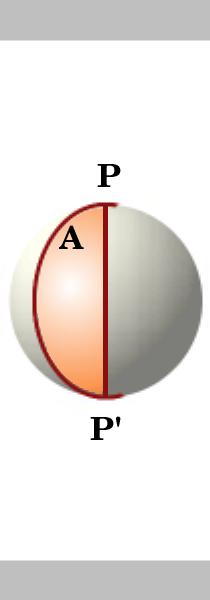
Lemma.

området av en lune på en sirkel av enhet for radius er dobbelt sin vinkel, det er hvis vinkelen på lune er En så sitt område er 2A. To store sirkler kryssende på antipodal punktene P og P’ del sfære og inn 4 lunes. Arealet av overflaten til en enhet sfære er $4\pi$.,

De områdene av lunes er proporsjonal til deres vinkler på P slik at arealet av et lune med vinkel A er

${\frac{A}{2\pi}\ganger {4\pi}= {2}}$

Øvelse 1.

Hva er de områdene av andre 3 lunes? Gjør din 4 områder legge opp til $4\pi$?

Sjekk dine svar her .

sidene i trekant ABC er segmenter av tre store ringer som faktisk kuttet overflaten av kulen inn i åtte sfærisk trekanter. Mellom de to store sirkler gjennom punkt A, er det fire vinkler., Vi merker en vinkel inne i trekanten ABC som En vinkel, og på samme måte de andre vinklene i trekanten ABC som vinkel B og vinkel C.

Roterende kule viser 8 trekanter

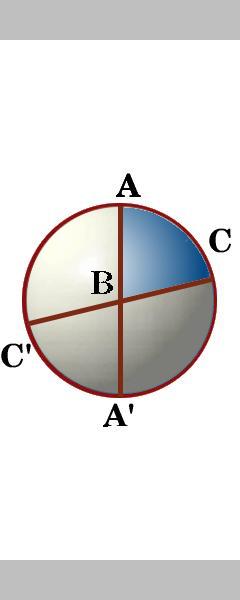
Øvelse 2

Roterende sfæren kan du nevne de åtte trekanter og si om noen av dem har det samme området? Sjekk dine svar her .

Teorem.

Vurdere en sfærisk trekant ABC på enheten sfære med vinklene A, B og C. Da arealet av trekanten ABC er

A + B + C – $\pi$.,

diagrammet viser en visning ser ned på halvkule som har linje gjennom AC som sin grense. Regionene merket Område 1 og Område 3 er lunes med vinklene A og C, henholdsvis. Vurdere lunes gjennom B og B’). Trekanten ABC er sammenfallende å trekant EN’B ° C’ så bow-tie formet skraverte området, merket Område 2, som er summen av de områdene av trekantene ABC og EN’BC’, er lik thearea av den lune med vinkel B, som er lik 2B.,

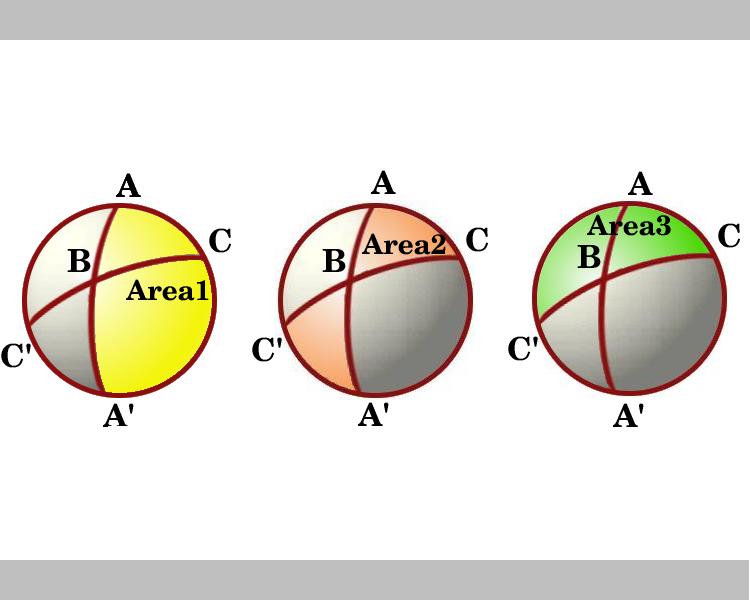
Så i diagrammet ser vi de områdene av tre lunes og, ved hjelp av lemma, og disse er:

Området 1 = 2A
Området 2 = 2B
– Området 3 = 2C

I å legge opp disse tre områdene vi har arealet av trekanten ABC tre ganger., Hence

3., Non-Euclidean Geometry

noen Ganger revolusjonerende oppdagelser er noe mer enn faktisk å se hva som har vært under våre neser hele tiden. Dette var tilfellet over oppdagelsen av Non-Euclidean Geometry i det nittende århundre. For noen år 2000 etter Euklids skrev sin «Elementer» i 325 F.KR folk prøvde å bevise parallell postulat som et teorem i geometri fra andre aksiomer, men alltid mislyktes, og thatis en lang historie., I mellomtiden matematikere var med sfærisk geometri hele tiden, en geometri som adlyder andre aksiomene av Euclidean Geometry og inneholder mange av de samme resultater, men hvor parallelle postulat, holder ikke. Alle sammen hadde de et eksempel på en Non-Euclidean Geometry under nesen.

Tenk på en linje L og et punkt P ikke på L. Det store spørsmålet er: «Hvor mange linjer kan trekkes gjennom P parallell til L?»I Euclidean Geometry svaret er `akkurat» og dette er en versjon av den parallelle postulat., Hvis summen av vinklene i hver trekant i geometri er $\pi$ radianer deretter parallelt postulat holder og vice versa, er det to egenskaper som er tilsvarende.

I sfærisk geometri, grunnleggende aksiomer som vi antar (reglene) er forskjellige fra Euclidean Geometry – dette er et Non-Euclidean Geometry. Vi har sett at i sfærisk geometri-vinkler i trekanter ikke alltid legge opp til $\pi$ radianer så vi ville ikke forvente den parallelle postulat å holde., I sfærisk geometri, rette linjer (linjer med kortest avstand eller geodesics)er store sirkler, og hver linje i geometri kutt annenhver linje i to punkter. Svaret på det store spørsmålet om parallels er`Hvis vi har en linje L og et punkt P ikke på L så det er ingen linjer gjennom P parallell til linjen L.,»

Den greske matematikere (for eksempel Ptolemaios c 150) beregnet målinger i rett vinkel på sfærisk trekanter og arbeidet med formler av sfærisk trigonometri og Arabiske matematikere (for eksempel Jabir ibn Aflah c 1125 og Nasir ed-din c 1250) utvidet til å jobbe enda mer. Formelen som er omtalt i denne artikkelen, ble oppdaget av Harriot i 1603 og som er publisert av Girard i 1629. Furtherideas av faget ble utviklet av Saccerhi (1667 – 1733).,

Alt dette gikk i stor grad un-merket av det 19. århundre oppdagere av hyperbolsk geometri, som er en Non-Euclidean Geometry hvor parallell postulat, holder ikke. I sfærisk geometri (også kalt elliptic geometri) vinklene i trekantene legge opp til mer enn $\pi$ radianer og i hyperbolsk geometri-vinkler i trekanter legge opp til mindre enn $\pi$ radianer.

For videre lesing se artikkel av Alan Beardon ‘Hvor mange Geometrier Er Det?»og artikkelen av Keith Carne ‘Rart Geometrier’ ., Det er noen praktiske aktiviteter som du kan prøve deg selv til å utforske disse geometrier videre for å bli funnet på http://nrich.maths.org/MOTIVATE/conf8/index.html