Menn. Jeg føler liksom at jeg liker det du sier.
Soc. Og jeg, Meno, i likhet med hva jeg sier.
fra Platons Meno
lengden av diagonalen av enheten kvadrat er lik kvadratroten av 2.
lengden av diagonalen av enheten kvadrat er lik √2. Vel, dette er ikke veldig gode nyheter. Alle som noen gang kom over Pytagoreisk teorem er klar over det faktum., I likebent høyre trekant med bena av lengde 1, hypotenuse, i henhold til Pytagoreisk teorem – 12 + 12 = (hypotenuse)2 – er faktisk av lengde √2. Motivasjonen for denne siden er ikke så mye at faktum i seg selv, men måten å vise det uten a ty til den berømte teorem. Ja, det kunne hevdes at Pytagoreisk teorem kan ha blitt for mye, kan du se et merkelig eksempel.
Et argument som går tilbake til figur tegnet av Sokrates i Platons Meno kan ha blitt kjent for å Pytagoras selv, selv om sistnevnte levde et århundre tidligere.,
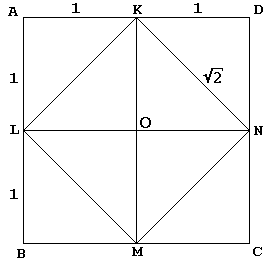
I dialogboksen, Sokrates, i sin vanlige måte, fører en ung slave til en konstruksjon av et kvadrat to ganger i området gitt en:
gitt square KLMN med sentrum O er første kuttet av sin diagonalene i 4 like store trekanter. Sokrates bygger KLMN til en større firkant ABCD som om reflekterer disse trekantene hver i sin hypotenuse. Slaven så innrømmer – og hvem ville ikke? – at firkanten ABCD er dobbelt så stor som square KLMN.
Sannheten bli fortalt, Sokrates’ firkant ABCD målt 4 på siden, slik at plassen KLMN hadde areal på 8., Det er klart at når vi begynner med kvadratet ABCD av side 2 (og dermed av område 4), square KLMN vil ha området av 2.
Nå, generelt, for et positivt tall A, √A er definert som tall som square er:
(√A)2.
På den andre siden, hver student områder vet, at arealet av et kvadrat av side b er lik b2. Det følger av dette at den side av et kvadrat med areal A er nøyaktig √A. Vi konkludere med at den siden av torget KLMN er lik √2. For en,
KN = √A.
Det sentrale punktet i argumentet er det faktum at, i diagrammet, KN spiller en dobbel rolle., Foruten å være en av sidene av plassen KLMN, det fungerer også som en diagonal av square OKDN. Sistnevnte er selvfølgelig en enhet square, som beviser vår påstand.
(Fra et litt annet perspektiv samme episode er nevnt andre steder.)
















Legg igjen en kommentar