Vis Mobile Merke Vis Alle Notater Skjule Alle Notater

Mobile Merke
Du ser ut til å være på en enhet med en «smal» skjerm bredde (dvs. er du sannsynligvis på en mobiltelefon). På grunn av matematikk på dette nettstedet er det beste utsikten i liggende modus. Hvis enheten ikke er i liggende modus mange av likningene vil kjøre ut på siden av enheten (bør være i stand til å bla for å se dem), og noen av menyvalgene vil være avskåret på grunn av den smale skjermen bredde.,

– Delen 4-11 : Lineær Tilnærming

I denne delen kommer vi til å ta en titt på et program som ikke er derivater, men av tangentlinjen til en funksjon. Selvfølgelig, å få tangentlinjen vi trenger å ta derivater, så på en eller annen måte dette er en anvendelse av derivater som godt.

\

Ta en titt på følgende grafen til en funksjon og dens tangentlinje.

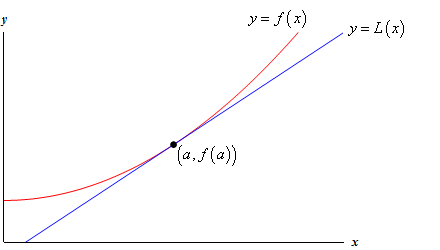
Så, hvorfor skulle vi gjøre dette? La oss ta en titt på et eksempel.,

Lineær tilnærming gjør en veldig god jobb med tilnærmet verdier av \(f\left( x \right)\) så lenge vi bo «i nærheten» \(x = a\). Men lenger og lenger bort fra \(x = a\) vi få det verre tilnærming er egnet til å bli. Det største problemet her er at hvor nær vi trenger for å holde seg til \(x = a\) for å få en god tilnærming vil være avhengig av både den funksjonen vi bruker, og verdien av \(x = a\) som vi bruker. Også, vil det ofte være noen enkel måte å forutsi hvor langt unna \(x = a\) vi kan få, og har fortsatt en «god» tilnærming.,

La oss ta en titt på et annet eksempel som er faktisk brukt ganske tungt i noen steder.

Dette er faktisk en noe viktig lineær tilnærming. I optikk denne lineær tilnærming er ofte brukt for å forenkle formlene. Dette lineær tilnærming er også brukt til å beskrive bevegelsen til en pendel og vibrasjoner i en streng.