Vis Mobile Merke Vis Alle Notater Skjule Alle Notater
– Del 3-1 : Parametriske Ligninger og Kurver
Til dette punktet (både Kalkulus jeg og Analyse II) vi har sett nesten utelukkende på funksjoner i form \(y = f\left( x \right)\) eller \(x = h\left( y \right)\), og nesten alle av formler som vi har utviklet krever at funksjoner i ett av disse to former. Problemet er at ikke alle kurver eller ligninger som vi ønsker å se på faller lett inn i dette skjemaet.
Ta for eksempel en sirkel. Det er lett nok til å skrive ned ligningen for en sirkel sentrert i origo med radius \(r\).,
\
Imidlertid, vil vi aldri være i stand til å skrive ligningen for en sirkel ned som en enkelt ligning i begge skjemaene ovenfor. Sikker på at vi kan løse for \(x\) eller \(y\) som følgende to formler vis
\
men det er faktisk to funksjoner i hver av disse. Hver formel gir en del av sirkelen.
\
Dessverre, vi vanligvis arbeider på hele sirkelen, eller rett og slett ikke kan si at vi kommer til å jobbe bare på en del av det. Selv om vi kan begrense ting ned til bare én av disse delene funksjonen er fortsatt ofte ganske ubehagelig å jobbe med.,
\
Denne tredje variabel er vanligvis merket med \(t\) (som vi gjorde her), men det trenger ikke å være selvfølgelig. Noen ganger vil vi begrense verdiene av \(t\), som vi vil bruke, og andre ganger gjør vi ikke. Dette vil ofte være avhengig av problemet og hva vi prøver å gjøre.
for Å hjelpe se bare hva en parametrisk kurve er late at vi har en stor tank med vann som er i konstant bevegelse, og vi slippe en ping-pong ball inn i tanken., Poenget \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\) vil da representere plasseringen av ping pong ballen i tanken på tidspunktet \(t\) og parametrisk kurve vil være en spore av alle steder i ping-pong-ball. Merk at dette er ikke alltid et riktig analogi, men det er nyttig først å bidra til å visualisere akkurat hva en parametrisk kurve er.
Skissere en parametrisk kurve er ikke alltid en enkel ting å gjøre. La oss ta en titt på et eksempel for å se en måte å skissere en parametrisk kurve., Dette eksemplet illustrerer også hvorfor denne metoden er vanligvis ikke det beste.
På dette punktet er vårt eneste alternativ for å tegne en parametrisk kurve er å plukke verdier av \(t\), koble dem til parametriske ligninger og deretter plotte punkter. Så, la oss plugg i noen \(t\)’s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Dessverre, det er ikke noe reelt svar på dette spørsmålet på dette punktet. Vi bare plukke \(t\)’s før vi er ganske sikre på at vi har fått et godt inntrykk av hvordan kurven ser ut. Det er dette problemet med å plukke «gode» verdier av \(t\) som gjør denne metoden med å skissere parametriske kurver en av de dårligere valg. Noen ganger har vi ikke noe valg, men hvis vi har et valg vi bør unngå det.
Vi vil diskutere en alternativ grafiske metoden i nyere eksempler som vil hjelpe til å forklare hvordan disse verdiene av \(t\) ble valgt.,
Vi har enda en idé å diskutere før vi faktisk skisse kurven. Parametriske kurver har en retning av bevegelse. Retningen av bevegelse er gitt ved å øke \(t\). Så, når parametrisk plotting av kurver, vi også inkluderer piler som viser retningen av bevegelse. Vi vil ofte gi verdien av \(t\) som ga spesifikke punkter på grafen i tillegg til å gjøre det klart verdien av \(t\) som ga det aktuelle punktet.
Her er skisse av dette parametrisk kurve.
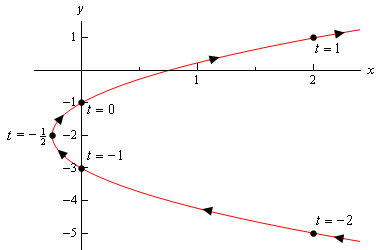
Så, det ser ut som vi har en parabel som åpnes til høyre.,
Før vi avslutter dette eksempelet er det en noe viktig og subtile poenget at vi trenger å diskutere første. Legg merke til at vi sørget for å inkludere en del av skissen til høyre på de punktene tilsvarer \(t = – 2\) og \(t = 1\) for å indikere at det er deler av skissen det. Vi hadde rett og slett sluttet å skissere på de punktene vi er som indikerer at det var ingen del av kurven til høyre på de poeng, og det helt klart vil være. Vi hadde bare ikke beregne noen av disse punktene.,
Dette kan virke som en uviktig poeng, men som vi vil se i neste eksempel er det viktigere enn vi kanskje tror.
Før du adresserer en mye enklere måte å skissere denne grafen la oss først ta opp spørsmålet om begrensninger på parameteren. I forrige eksempel hadde vi ikke har noen begrensninger på parameteren. Uten begrensninger på parameteren grafen vil fortsette i begge retninger som vist i skissen ovenfor.
Vi har ofte begrensninger på parameteren men, og dette vil påvirke skisse av parametriske ligninger., For å se denne effekten la oss se en liten variant av forrige eksempel.
Merk at den eneste forskjellen her er tilstedeværelsen av grensene på \(t\). Alle disse grensene gjøre er å fortelle oss at vi ikke kan ta hvilken som helst verdi av \(t\) utenfor dette området. Derfor parametrisk kurve vil bare være en del av kurven ovenfor. Her er parametrisk kurve for dette eksemplet.,
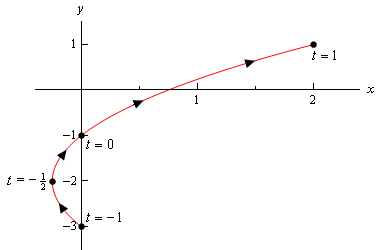
legg Merke til at med denne skissen vi startet og stoppet skissen til høyre på de punktene som stammer fra slutten poeng av omfanget av \(t\)’s. Kontrasten denne med skissen i forrige eksempel, der vi hadde en del av skissen til høyre for «start» og «end» – poeng som vi har beregnet.
I dette tilfellet kurven starter på \(t = – 1\) og ender på \(t = 1\), mens det i forrige eksempel kurven egentlig ikke starter på riktig mest poeng at vi rekna ut., Vi må være tydelige i våre skisser hvis kurven starter/slutter rett på et punkt, eller hvis det punktet var det bare den første/siste som vi har beregnet.
Det er nå på tide å ta en titt på en enklere metode med å skissere dette parametrisk kurve. Dette er en metode som bruker det faktum at i mange, men ikke alle, tilfeller kan vi faktisk eliminere parameter fra de parametriske ligningene og får en funksjon med bare \(x\) og \(y\). Vil vi noen ganger kaller dette algebraisk ligning for å skille den fra den opprinnelige parametriske ligninger., Det vil være to små problemer med denne metoden, men det vil være enkelt å løse disse problemene. Det er viktig å merke seg imidlertid at vi ikke alltid være i stand til å gjøre dette.
Akkurat hvor vi eliminere parameteren vil være avhengig av den parametriske ligninger som vi har fått. La oss se på hvordan å eliminere parameter for å angi parametriske ligninger som vi har jobbet med til dette punktet.
Komme en skisse av parametrisk kurve når vi har fjernet parameteren virker ganske enkel. Alt vi trenger å gjøre er grafen til ligningen som vi fant ved å eliminere parameter., Som nevnt allerede imidlertid, det er to små problemer med denne metoden. Den første er retning av bevegelse. Ligningen som involverer bare \(x\) og \(y\) vil IKKE gi retning av bevegelse av parametrisk kurve. Dette er vanligvis et enkelt problem å fikse likevel. La oss ta en rask titt på derivater av de parametriske ligningene fra forrige eksempel. De er
\
Merk at \(x\) derivat er ikke så nyttig for denne analysen som det vil være både positive og negative, og dermed \(x\) vil være både stigende og synkende avhengig av verdien av \(t\)., Det hjelper ikke med retning, mye som følge kurven i begge retninger vil vise både øke og redusere \(x\).
I noen tilfeller bare én av ligninger, slik som i dette eksemplet, vil gi retning, mens i andre tilfeller enten man kunne brukes. Det er også mulig at det i enkelte tilfeller, både derivater ville være nødvendig for å bestemme retning. Det vil alltid være avhengig av den enkelte sett av parametriske ligninger.,
Det andre problemet med å eliminere parameteren er best illustrert ved et eksempel som vi skal kjøre inn i dette problemet i den gjenværende eksempler.
Okei, det var en veldig lang eksempel. De fleste av disse typer problemer er ikke så lang. Vi hadde mye å diskutere i dette slik at vi kunne få et par viktige ideer ut av veien. Resten av eksemplene i dette avsnittet bør ikke ta så lang tid å gå gjennom.
Nå, la oss ta en titt på et annet eksempel som vil illustrere et viktig ideen om parametriske ligninger.,
Så, som vi så i de to siste eksemplene to sett av parametriske ligninger som på noen måte gav den samme grafen. Likevel, fordi de spores ut grafen et forskjellig antall ganger vi egentlig ikke trenger å tenke på dem som ulike parametriske kurver i alle fall i noen måte. Dette kan virke som en forskjell at vi ikke trenger å bekymre deg om, men som vi skal se i senere avsnitt kan dette være en svært viktig forskjell. I noen av de senere avsnitt skal vi trenger en kurve som er undersøkt ut nøyaktig én gang.,
Før vi går videre til andre problemer la oss kort erkjenner hva som skjer ved å endre \(t\) til en nt i disse typer parametriske ligninger. Når vi har å gjøre med parametriske ligninger som involverer bare sines og cosines, og de har begge det samme argumentet om vi endrer argumentet fra \(t\) til nt-vi bare endre hastigheten som kurven er spores ut. Hvis \(n > 1\) vi vil øke hastigheten og om \(n < 1\) vi vil redusere hastigheten.
La oss ta en titt på et par eksempler.,
Til dette punktet har vi sett eksempler på at ville spore ut den komplette grafen som vi fikk ved å eliminere parameteren hvis vi tok et stort nok utvalg av \(t\)’s. Men i forrige eksempel har vi nå sett at dette vil ikke alltid være tilfelle. Det er mer enn mulig å ha et sett av parametriske ligninger som vil kontinuerlig spore ut bare en del av kurven. Vi kan vanligvis finne ut om dette vil skje ved å se for begrensninger på \(x\) og \(y\), som er pålagt oss opp av den parametriske ligningen.,
vil Vi ofte bruke parametriske ligninger for å beskrive banen til et objekt eller en partikkel. La oss ta en titt på et eksempel på det.
Vi bør gi en liten advarsel på dette punktet. På grunn av ideer som er involvert i dem vi konsentrert på parametriske kurver som retraced deler av kurven mer enn én gang. Ikke gjør det, men får altfor låst inn ideen om at dette vil alltid skje. Mange, om ikke de fleste parametriske kurver vil bare spore ut en gang. Den første vi har sett på er et godt eksempel på dette. Som parametrisk kurve vil aldri gjenta en del av seg selv.,
Det er et siste tema som skal diskuteres i denne delen før du går videre. Så langt vi har startet med parametriske ligninger og eliminert parameter for å bestemme parametrisk kurve.
Imidlertid, det er tider hvor vi ønsker å gå den andre veien. Gitt en funksjon eller ligningen vi kan være lurt å skrive ned et sett av parametriske ligninger for det. I slike tilfeller vil vi si at vi parameterize funksjonen.
Hvis vi tar Eksempler 4 og 5 som eksempler kan vi gjøre dette for ellipser (og dermed sirkler)., Gitt ellipse
\
et sett av parametriske ligninger for det ville være,
\
Dette settet av parametriske ligninger vil spore ut ellipse starter på det punktet \(\left( {a,0} \right)\), og vil spore i en moturs og vil spore ut nøyaktig én gang i serien \(0 \le t \le 2\pi \). Dette er en ganske viktig sett av parametriske ligninger som det brukes kontinuerlig i noen fag med håndteringen av ellipser og/eller sirkler.
Hver kurve kan være parameterized på mer enn en måte. Noe av det følgende, vil også parameterize samme ellipse.,
\
tilstedeværelsen av \(\omega \) vil endre hastigheten som ellipse roterer som vi så i Eksempel 5. Merk også at de to siste vil spore ut ellipser med klokkens retning av bevegelse (det kan hende du ønsker å verifisere dette). Vær også oppmerksom på at de ikke alle starter på samme sted (hvis vi tenker på \(t = 0\) som utgangspunkt at det er).
Det er mange flere parametere av en ellipse selvfølgelig, men du får ideen. Det er viktig å huske at hver parameterization vil spore ut kurve gang med potensielt forskjellige utvalg av \(t\)’s., Hver parameterization kan rotere med forskjellige retninger av bevegelse og kan starte på forskjellige steder.
du kan finne at Du trenger en parameteriseringen av en ellipse som starter på et bestemt sted, og har en spesiell retning av bevegelse og så vet du nå at med litt arbeid kan du skrive ned et sett av parametriske ligninger som vil gi deg den oppførsel som du er ute etter.
Nå, la oss skrive ned et par andre viktige parametere og alle kommentarene om retningen av bevegelse, utgangspunkt, og omfanget av \(t\)’s for en spore (hvis aktuelt) er fortsatt sann.,
for det Første, fordi en sirkel er noe mer enn et spesielt tilfelle av en ellipse vi kan bruke parameteriseringen av en ellipse å få den parametriske ligninger for en sirkel sentrert i origo med radius \(r\) som godt. En mulig måte å parameterize en sirkel er,
\ \
På dette punktet kan det synes det ikke alle som nyttig å gjøre en parameteriseringen av en funksjon som dette, men det er mange tilfeller der vil det faktisk være enklere, eller kan det også være nødvendig å arbeide med å parameterisere i stedet for funksjonen selv., Dessverre, nesten alle av disse tilfellene oppstår i en Kalkulus III kurs.
















Legg igjen en kommentar