Trekant Figur Vinkel-Side-Vinkel (ASA)
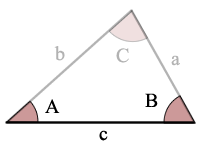
A = vinkel A
B = vinkel B
C = vinkel C
a = siden en
b = side b
c = siden c
P = omkretsen
s = semi-perimeter
K = areal
r = radius i innskrevet sirkel
R = radius av omskrevet sirkel
Kalkulator Bruk
Hver alternativ beregning, som vist nedenfor, har sub-kuler som liste sekvensen av metodene som brukes i denne kalkulatoren for å løse for ukjent vinkel og siden verdiene inkluderer Summen av Vinklene i en Trekant, Lov av Sines og Lov av Cosines., Disse er IKKE de ENESTE sekvenser du kan bruke til å løse denne typen problemer.
- Se også disse Trigonometri Kalkulatorer:
- Lov av Cosines Kalkulator
- Lov av Sines Kalkulator
Løse Trekant Teoremer
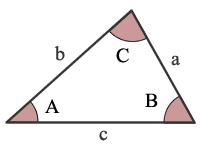
AAA er vinkel, Vinkel, Vinkel
Angi de tre vinklene i en trekant ikke unikt identifisere en trekant. Derfor, angi to vinkler av en tringle lar deg beregne den tredje vinkelen bare.,
Gitt størrelser av 2 vinkler i en trekant kan du beregne størrelsen av den tredje vinkelen. Totalt vil lik 180° eller π radianer.
C = 180° – A – B (i grader)
C = π – A – B (i radianer)
AAS er vinkel, Vinkel, Side
Gitt størrelse 2 vinkler og 1 side overfor en av de gitte vinkler, kan du beregne størrelsen på de gjenværende 1 vinkel og 2 sider.
bruk Summen av Vinklene Regel å finne en annen vinkel, og deretter
bruk Loven om Sines å løse for hver av de to andre sidene.,
ASA er Vinkel, Side -, Vinkel
Gitt størrelse 2 vinkler og størrelsen på den siden som er i mellom disse 2 vinkler du kan beregne størrelsen på de gjenværende 1 vinkel og 2 sider.
bruk Summen av Vinklene Regel å finne en annen vinkel, og deretter
bruk Loven om Sines å løse for hver av de to andre sidene.,
RÆVA (eller SSA) er Vinkel, Side, Side
Gitt størrelsen på 2 sider (a og c, hvor a < c) og størrelsen på vinkelen En som ikke er i mellom disse 2 sider du kan være i stand til å beregne størrelsen på de gjenværende side 1 og 2 vinkler, avhengig av følgende forhold.,f Cosines å løse for hver av de to andre vinkler
stede 2 komplette løsninger
Eksempel: 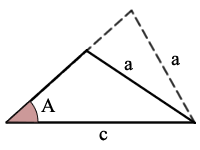
sin(A) = a/c, det er en mulig trekant
bruk Loven om Sines å løse for en vinkel, C
bruk Summen av Vinklene Regel å finne en annen vinkel, B
bruk Loven om Sines å løse for den siste siden, b
Eksempel: 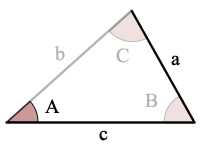
sin(A) > a/c, det er ikke mulig trekanter
Feil Merknad: sin(A) > a/c, så det er ingen løsninger og ingen trekant!,
Eksempel: 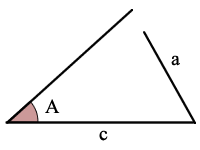
SAS er Side, Vinkel, Side
Gitt størrelsen på 2 sider (c og a) og størrelsen på vinkelen B, som er i mellom disse 2 sidene kan du beregne størrelsen på de gjenværende side 1 og 2 vinkler.
bruke Loven for Cosines å løse for de resterende siden, b
finne ut hvilken side, a eller c, er minste og bruke Loven av Sines å løse for størrelsen på motsatt vinkel, A eller C, henholdsvis.,
bruk Summen av Vinklene Regel å finne den siste vinkel
SSS er Side, Side, Side
Gitt størrelsen på de 3 sidene kan du beregne størrelser på alle 3 vinklene i trekanten.
bruke Loven for Cosines å løse for vinkler. Du kan også bruke Summen av Vinklene Regel å finne den endelige vinkel når du vet at 2 av dem.,synd-1
Lov av Cosines
Hvis a, b og c er lengden på bena av en trekant på motsatt side til vinklene A, B og C henholdsvis; da loven av cosines uttaler:
a2 = c2 + b2 – 2bc cos A, løse for cos A cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, løse for cos B, cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, løse for cos C, cos C = ( a2 + b2 – c2 ) / 2ab
Løse, for eksempel, for en vinkel, A = cos-1
Andre Trekanten Egenskaper
Trekant omkretsen, P = a + b + c
Trekant semi-perimeter, s = 0.,5 * (a + b + c)
Triangel, K = √
Radius av innskrevet sirkel i trekanten, r = √
Radius av omskrevet sirkel rundt trekanten, R = (abc) / (4K)
Referanser/ Videre Lesning
Weisstein, Eric W. «ASS-Teoremet.»Fra MathWorld– En Wolfram Web-Ressurs. ASS-Teoremet.
Matematikk er Gøy – Løse SAS Trekanter
















Legg igjen en kommentar