Del på

Innhold (Klikk for å hoppe over til den delen):

  1. Alt om…
    • Mean
    • Modus
    • Median
  2. Hvordan finne gjennomsnitt, median og modus for hånd.
  3. Finne gjennomsnitt, median og modus med Teknologi:
    • SPSS
    • TI83

Oversikt

Fast på hvordan å finne gjennomsnitt, median, & modus i statistikken?,

  1. De mener er gjennomsnittet av et datasett.
  2. modus som er den mest vanlige tall i et datasett.
  3. medianen er den midterste av sett med tall.

Av tre, som de mener er de eneste som krever en formel. Jeg liker å tenke på det i andre ordlisten betydningen av ordet (som i, det er mener, i motsetning til nice!). Det er fordi, i forhold til de to andre, det er ikke så lett å jobbe med.,


Tips å huske forskjellen

etter å Ha problemer med å huske forskjellen mellom gjennomsnitt, median og modus? Her er et par tips som kan hjelpe. Du kan også sjekke ut veilederne på Chegg.com (de første 30 minuttene er gratis!).

  • «A la mode» er et fransk ord som betyr fasjonable ; Det viser også til en populær måte å tjene iskrem. Så «Modus» er den mest populære eller fasjonable medlem av et sett med tall. Ordet Modus er også som de Fleste.,
  • «Slemme» krever at du utføre aritmetiske operasjoner (legge alle tallene og dele) slik at de «mener» en.
  • «Median» har samme antall bokstaver i «Midten».

Fortsatt ikke er sikker på hva forskjellen er mellom de tre? Se videoen eller les videre for mer info:

Vennligst godta statistikk, markedsføring informasjonskapsler for å se denne videoen.

Det Betyr

Mener vs. Median
Mener vs., Gjennomsnittlig
Bestemt «Betyr» som vanligvis brukes i Statistikk
Andre Typer

Mener vs Median

Begge er tiltak av hvor midten av et datasett ligger (kalt «Sentral-Tendens» i statistikk), men de er vanligvis forskjellige tall. Ta For eksempel denne listen med tall: 10, 10, 20, 40, 70.

  • mean (uformelt, «gjennomsnittlig») er funnet ved å legge til alle sammen tallene og dividere med antall elementer i settet: 10 + 10 + 20 + 40 + 70 / 5 = 30.
  • medianen er funnet ved å bestille den fra lavest til høyest, og å finne den eksakte midten., Medianen er bare midten antall: 20.

noen Ganger de to vil være det samme nummeret. For eksempel, data set 1, 2, 4, 6, 7 har et gjennomsnitt på 1 + 2 + 4 + 6 + 7 / 5 = 4 og en median (midtre) på 4.

Mener vs Gjennomsnitt: Hva er Forskjellen?

Når du først startet i matematikk, ble du sannsynligvis lært at en gjennomsnittlig var en «mellomliggende» beløp for et sett med tall. Du lagt opp tallene, dividert med antall elementer du kan og voila! du får gjennomsnittet. For eksempel gjennomsnittet av 10, en 5 og 20 er:

10 + 6 + 20 = 36 / 3 = 12.,

du begynte å studere statistikk og plutselig er «gjennomsnittlig» heter nå det betyr. Hva skjedde? Svaret er at de har samme betydning(de er synonymer).

når Det er sagt, teknisk sett, ordet betyr er kort for aritmetisk gjennomsnitt. Vi bruker forskjellige ord i statistikken, fordi det er flere ulike typer virkemidler, og de gjør forskjellige ting.

Bestemt «Betyr» som vanligvis brukes i Statistikk

vil Du sannsynligvis kommet over disse i statistikken din klasse., De har en meget snever betydning:

  • Bety for den tilfeldige fordeling: brukt med sannsynlighetsfordelinger, spesielt med den Sentrale grensesetningen. Det er et gjennomsnitt av et sett av fordelinger.
  • Eksempel bety: den gjennomsnittlige verdien i en prøve.
  • populasjonsgjennomsnitt: gjennomsnittlig verdi i en befolkning.

Kenney, J. F. og Holde, E. S. Matematikk, Statistikk, Pkt. 1, 3. utg. Princeton, NJ: Van Nostrand, 1962.

Andre Typer

Det er også andre typer av midler, og du vil bruke dem i ulike grener av matematikk., De fleste har svært smale programmer til felt som økonomi eller fysikk, hvis du er i elementær statistikk har du sannsynligvis ikke vil samarbeide med dem.

Dette er noen av de vanligste typene du kommer over.

  1. Vektet gjennomsnitt.
  2. Harmonisk mener.
  3. Geometriske mener.
  4. Matematikk-Geometriske mener.
  5. Root-Mean Square mener.
  6. Heronian mener.
  7. Grafisk Bety

  1. Vektet gjennomsnitt

    Dette er ganske vanlig i statistikk, spesielt når man studerer bestander., I stedet for hvert datapunkt bidrar like mye til den endelige gjennomsnitt, noen data poeng bidra mer enn andre. Hvis alle vekter er lik, så vil dette lik det aritmetiske gjennomsnittet. Det er visse tilfeller når dette kan gi feil informasjon, som vist ved Simpson Paradoks.

  2. Harmonisk Bety

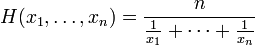
    harmonisk formel.

    for Å finne det:

    1. Legg til reciprocals av tallene i settet., For å finne en gjensidig, snu brøkdel slik at telleren blir nevneren og nevneren blir telleren. For eksempel, den gjensidige av 6/1 er 1/6.
    2. Dele svaret med antall elementer i settet.
    3. Ta den gjensidige resultat.

    harmonisk mener er brukt ganske mye i fysikk. I noen tilfeller involverer priser og forholdstall det gir et bedre gjennomsnitt enn det aritmetiske gjennomsnittet. Du finner også bruker i geometri, økonomi og informatikk.,

  3. Geometrisk Middelverdi


    Denne typen har svært smal og spesifikk bruk i økonomi, samfunnsvitenskap og teknologi. For eksempel, la oss si at du eier aksjer som tjener 5% det første året, 20% andre året, og 10% i det tredje året. Hvis du ønsker å vite gjennomsnittlig avkastning, kan du ikke bruke det aritmetiske gjennomsnitt. Hvorfor? Fordi når du er å finne priser of return du multiplisere, ikke å legge til. For eksempel, det første året er du multiplisere med 1.05.,

  4. Matematikk-Geometrisk Middelverdi

    Dette brukes for det meste i kalkulus og i maskin beregning (dvs. som grunnleggende for mange pc-beregninger). Det er relatert til omkretsen av en ellipse. Når det først ble utviklet av Gauss, det ble brukt til å beregne planetenes baner. Det aritmetiske-geometrisk er (ikke overraskende!) en blanding av den aritmetiske og geometriske gjennomsnitt. Regnestykket er ganske komplisert, men du kan finne en relativt enkel forklaring av regnestykket her.,

  5. Root-Mean Square

    Det er svært nyttig i felt som studerer sinus bølger, som elektroteknikk. Denne typen er også kalt kvadratisk snitt. Se: Kvadratisk Middelverdi / Root Mean Square.

  6. Heronian Bety

    Brukt i geometri for å finne volumet av en pyramideformet frustum. En pyramideformet frustum er i utgangspunktet en pyramide med spissen skiver av.

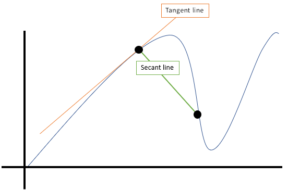
  7. Grafisk Bety

    et Annet navn for skråningen av sekant linje: tilsvarende gjennomsnittlig endring mellom to punkter.,

Hva er Modus?

Den modus som er den mest vanlige tall i et sett. For eksempel modus i dette settet av tall er 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33

Hva er Medianen?

medianen er det midterste tallet i et datasett. For å finne medianen liste over dine data poeng i stigende rekkefølge, og deretter finne tallet., Tallet i dette settet er 28 som det er 4 tallene nedenfor og 4 tallene ovenfor:
23, 24, 26, 26, 28, 29, 30, 31, 33

Hvordan finne gjennomsnitt, median og modus for hånd: Trinn

Hvordan finne gjennomsnitt, median og modus: MODUS

Hvordan finne gjennomsnitt, median og modus: BETYR

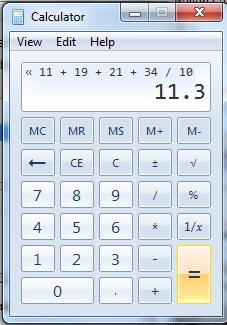
Dividere summen med antall elementer for å finne de mener.

Hvordan finne gjennomsnitt, median og modus: MEDIAN

Hvis du hadde en merkelig nummer i trinn 3, kan du gå til trinn 5. Hvis du hadde et partall, gå til trinn 6.,

Tips: Du kan ha mer enn én modus. For eksempel, modus 1, 1, 5, 5, 6, 6 er 1, 5, og 6.

Som forklaring? Sjekk ut Praktisk talt Juks Statistikk Håndbok, som har hundrevis av flere trinn-for-trinn-løsninger, akkurat som denne!

SPSS Bety modus median

for å finne SPSS bety modus median, vil du trenger å bruke Frekvens kategorien. Det virker litt ulogisk, men Beskrivende Statistikk-fanen gir deg ikke muligheten til å finne modus eller median.,

SPSS har en veldig lignende grensesnitt til Microsoft Excel. Derfor, hvis du har brukt Microsoft Excel før, vil du raskt tilpasse seg til SPSS.

SPSS Bety Modus Median: Trinn

Se videoen eller lese trinnene nedenfor:

Vennligst godta statistikk, markedsføring informasjonskapsler for å se denne videoen.

Eksempel spørsmålet: Finn SPSS bety modus median for følgende datasett: 20,23,35,66,55,66

Trinn 1: Åpne SPSS. I «Hva ønsker du å gjøre?»dialogboksen, klikk på «skriv inn data» – knappen, og klikk «OK.»Et nytt regneark vil åpne., Merk: Hvis du har valgt deg ut av den første skjermen, kan du ikke ser dette alternativet. I så fall, kan du bare begynne på Trinn 2.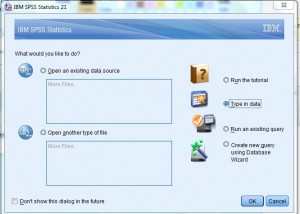

Trinn 2: Skriv inn data i regnearket. Du kan skrive inn data i en kolonne eller flere kolonner hvis du har flere datasett. For dette eksempelet, type 20, 23, 35, 66, 55, 66 i kolonne 1. Ikke la mellomrom mellom data (dvs. ikke la noen tomme rader).

Trinn 2: Klikk «Analysere» hold markøren over «Beskrivende Statistikk» og deretter «Frekvenser.,»

Trinn 3: Klikk på «Statistikk» og deretter merker du av i boksene «mener», «modus», og «median.»Klikk «Fortsett» to ganger (velg «ingen» som diagramtype i det andre vinduet).
Merk: I enkelte versjoner av SPSS, kan du bare å klikke på «Fortsett» når du er og det kan ikke gi deg et alternativ for diagramtype.

frekvensen resultatene vil vises som output. Den øverste delen av produksjonen vil vise mener, modus og median.

Hvis du blar ned, frekvens tabellen vil også vise deg modus., Modusen er definert i statistikk som antall med høyest frekvens (for denne eksempeldata, nummer vises de er 66, med to resultater i kolonnen frekvens).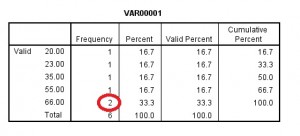

TI-83 Gjennomsnitt, Median og Modus

Finne den TI 83 betyr eller TI-83 median fra en liste av data kan gjøres på to måter: ved å legge inn en liste av data, eller ved å bruke home-skjermbildet for å skrive inn kommandoer., Ved hjelp av listen funksjonen er like enkelt som å skrive inn data på hjem-skjermen, og det har den ekstra fordelen at du kan bruke dataene til andre formål etter at du har beregnet dine gjennomsnitt, modus og median (for eksempel, ønsker du kanskje å opprette en TI-83 histogram).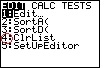

Trinnene for Gjennomsnitt, Median og Modus på TI 83

Se videoen for gjennomsnittlig og median eller les trinnene under (for-modus, kan du se dette notatet):

Vennligst godta statistikk, markedsføring informasjonskapsler for å se denne videoen.

Trinn 1: Angi de ovennevnte data inn i en liste., Trykk på STAT-knappen og trykk deretter på ENTER. Skriv inn det første tallet (1250), og trykk deretter på ENTER. Fortsett å legge inn tall, trykker du på ENTER-knappen etter hver oppføring.

Trinn 2: Trykk på STAT-knappen.

Trinn 3: Trykk på pil høyre-knappen for å markere «Calc.»

Trinn 4: Trykk ENTER for å velge «1-Var Stats» og deretter skriver du inn i listen navn. For eksempel, for å taste inn L1 trykker du på og .

Trinn 5: Trykk ENTER igjen. Kalkulatoren vil returnere mener, x. For denne listen av data, TI-83 mener er 884.05 fot (avrundet til 3 desimaler).

Trinn 6: Pil ned til du ser «Med.,»Dette er de TI 83 median; for de ovennevnte data, median er 813.05 føtter.

Merk: TI-83 plus ikke har en innebygd i modus funksjon, men når du har skrevet inn din liste, det er ganske lett å få øye på-modus: det er bare tall som forekommer oftest i settet. Ikke sikker på det? Les mer om modus her.

det er det!

Mistet din guidebok? Last ned en ny her på TI hjemmeside.

——————————————————————————

Trenger hjelp med lekser eller test spørsmål?, Med Chegg Studere, kan du få trinn-for-trinn-løsninger til dine spørsmål fra en ekspert på feltet. De første 30 minutter med en Chegg veileder er gratis!