Konvekse og Konkave Polygoner

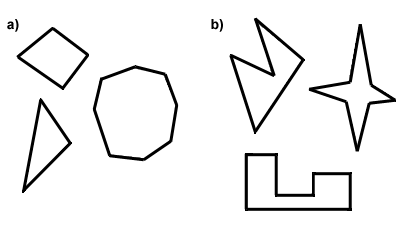
Hver polygon er enten konveks eller konkav. Thedifference mellom konvekse og konkave polygoner ligger i tiltak av deres vinkler. For et polygon til å beconvex alle dens indre vinklene må være mindre enn 180 grader. Ellers, polygon isconcave. En annen måte å tenke på det er dette: diagonalene av en convexpolygon vil alle være på innsiden av den polygon, mens enkelte diagonaler av en konkav polygon vil ligge utenfor polygon, på eksteriøret., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

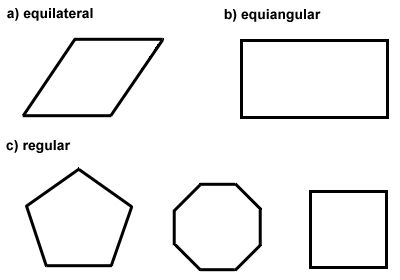
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Når et polygon er både likesidet og equiangular, det kalles et regulært polygon. Et kvadrat er et eksempel på et regulært polygon. Midten av et regulært polygon er det punktet som alle hjørner av polygon er like langt. Regulære polygoner har spesielle egenskaper som vi vil utforske i neste avsnitt. Nedenfor er noen eksempler på equiangular, likesidet, og regulære polygoner.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.