En vektor har magnitude (hvor lenge det er) og retning:
Her er to vektorer:

De kan bli multiplisert med «Prikk-Produktet» (se også Cross-Produkt).,
Vi kan beregne Prikk-Produktet av to vektorer på denne måten:

a · b = |a| × |b| × cos(θ)
Hvor:
|en| er størrelsen (lengden) av en vektor
|b| er størrelsen (lengden) av en vektor b
θ er vinkelen mellom a og b
Så vi multiplisere lengden av en ganger lengden av b, og deretter multiplisere med cosinus til vinkelen mellom a og b
ELLER vi kan beregne det på denne måten:
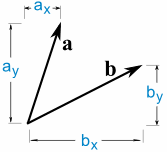
a · b = ax × bx + ay × av
Så vi multiplisere x, må du multiplisere den y-tallet, deretter på legg til.,
Begge metodene fungerer!
Og resultatet er et tall (kalt en «skalar», så vi vet det er ikke en vektor).
Merk: du kan bruke Vektor Calculatorto hjelpe deg.
Hvorfor cos(θ) ?
OK, for å multiplisere to vektorer er det fornuftig å multiplisere deres lengder sammen, men bare når de peker i samme retning.,
Så vi gjør en «peker i samme retning som de andre ved å multiplisere av cos(θ):
 |
 |
|
| Vi tar del av en som ligger ved siden av b |
Som skinner et lys for å se hvor skyggen ligger |
SÅ vi multiplisere !,
Rett Vinkel
Når to vektorer er i rett vinkel til hverandre prikk-produktet er null.
Dette kan være en nyttig måte å finne ut om to vektorer er i rett vinkel.
Tre eller Flere Dimensjoner
alt Dette fungerer fint i 3 (eller flere) mål, også.
Og kan faktisk være veldig nyttig!
jeg prøvde en beregning som det en gang, men jobbet i alle vinkler og avstander … det var veldig hardt, engasjert mange trigonometri, og hjernen min vondt. Metoden ovenfor er mye enklere.,
Cross Produktet
Prikk-Produktet gir en skalar (vanlige tall) svar, og blir noen ganger kalt skalar produktet.
Men det er også Cross Produktet som gir en vektor som et svar, og det er noen ganger kalt vektor-produkt.

















Legg igjen en kommentar