I dag tar vi en titt på de mest populære alternativene prismodell. Black-Scholes-Modellen, også kjent som Black-Scholes-Merton-metoden, er en matematisk modell for å prise opsjoner. Det fungerer ved å estimere variasjonen i finansielle instrumenter. Teknikken baserer seg på antagelsen om at prisene følge en lognormal fordeling. Basert på dette, det kommer verdien av en opsjon.,

Det er mer egnet for bane-uavhengige valg, som investorene ikke kan utøve før forfallsdato. Dette gjør den forskjellig fra den Binomiske opsjonsprisingsmodell, som er en risiko-nøytral metode for verdsettelse sti-avhengige valg (f.eks., American valg).

Analytikere og investorer vurdere Black Scholes til å være et av de viktigste begreper i moderne finansteori.

Innført i 1973 i Journal of Political Economy, med Fischer Svart og Myron Scholes, og senere bygget på med Robert Merton, modellen som vant nobelprisen i økonomi i 1997.,

modellen følger en differensial-likningen, som vi bruker til å løse for valg’ priser. Vi bruker standard variant av modellen for Europeisk stil valg. Black Scholes er ikke egnet for Amerikansk stil valg, som det ikke vurdere investorer kan utøve disse alternativene når som helst før holdbarhetsdatoen.

Den metoden forutsetter prisen på den underliggende aksjen følger en lognormal fordeling, så det kan ikke være negativ. Fordelingen modellen baserer seg på er basert på Brownske bevegelser, en teori for å forutsi naturlig forekommende tilfeldige fenomener.,

Vi bruke modellen til å beregne et estimat for en alternativ pris, med følgende informasjon:

  • gjeldende pris;
  • innløsningskurs;
  • Tid til utløp;
  • Forventede utbyttet;
  • Forventet rente; og
  • Forventet volatilitet.

Først, modellen ikke vurdere effekten av utbytte utbetalinger. Derfor er det ofte tilpasset til å gjøre det ved å bestemme ex-utbytte dato verdien av det underliggende aktiva., Utbytte yield har effekt av å redusere den gjeldende aksjekursen fordi alternativet holderen forgoes utbytte.

Forutsetninger

Black-Scholes modellen fungerer bare hvis vi gjør visse forutsetninger.,s oppstå under valget levetid (dette var en forutsetning i den første modellen, som analytikere har siden eliminert ved å legge utbyttet i modellen formel);

  • markedene er helt effektiv, betyr at vi kan ikke forutse sine bevegelser;
  • Kjøp og salg av opsjoner innebærer ingen transaksjonskostnader;
  • Både volatilitet i den underliggende eiendelen og risikofri rente forblir konstant inntil utløpsdatoen, der er ikke riktig, som i virkeligheten volatilitet skift med tilbud og etterspørsel, og

  • avkastning på den underliggende aktiva følger en normalfordeling.,

    • Black Scholes Formel

    modellen formelen er ganske komplisert matematisk, noe som ikke er et spesielt tema, som vi kan ta i bruk spesialiserte verktøy for å beregne det for oss. Men det er fortsatt viktig å forstå hvordan det fungerer.,

    for Å beregne prisen for en kjøpsopsjon, under Black-Scholes-modellen, kan vi bruke følgende ligning:

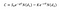
    Hvor:

    • S0 er på lager pris;
    • e er den eksponentielle antall;
    • q er utbyttet andel;
    • T er sikt (ett år vil være T=1, mens seks måneder vil være T=0.,5);
    • N(d1) er deltaet samtale-alternativet, som betyr at endringen i samtalen pris over endringen i aksjekursen;
    • K er innløsningskurs;
    • r er risikofri rente, og
    • N(d2) er sannsynligheten for at fremtidig aksjekurs vil være høyere enn strike pris, sannsynligheten for at vi vil utøve opsjonen.

    den Ene siden er aksjekursen multiplisert med den kumulative standard normalfordeling av d1, og den andre — strike pris, neddiskontert til tidspunkt T og deretter multiplisert med den kumulative standard normalfordeling av d2.,

    Hvor vi kan beregne d1 og d2 med følgende formler:

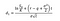
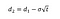
    Hvor σ er volatiliteten i avkastningen på den underliggende aktiva.,

    Vi kan bruke den samme logikken for en salgsopsjon:

    Meld deg på vårt Nyhetsbrev for å få en GRATIS Excel Benchmark Analyse Mal

    Eksempel Black Scholes Beregning

    for Å bedre illustrere konseptet bak Black-Scholes-Modellen, vil vi ta en titt på følgende modell. Vi starter med modellen innganger., Som diskutert ovenfor, trenger vi følgende seks variabler for å beregne anrop og sette alternativet verdier.

    Neste, vil vi beregne valg » parametere. Starter med d1, får vi 0.39 fra vår modell forutsetninger.

    for Å beregne det, kan vi ganske enkelt overføre formelen for d1 til Excel.,

    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    Vi kan ansette Samtalen-Sette Paritet regel å sjekke om formler og beregninger er riktige.

    Nå som vi har vår modell for å beregne kjøps-og salgsopsjoner priser, vi kan gå et skritt videre og se på hvordan de ulike parametere påvirker resultatene av vår modell., Data Tabell funksjonalitet i Excel er et flott verktøy for å lage noen sensitivitetsanalyse tabeller for våre variabler. Du kan lære å bruke Data Bord i vår sensitivitetsanalyse artikkelen.

    La oss se på Lager Pris hvis den endres fra €10 og €100, og hvordan det påvirker Anrop og Sette verdier. Vi legger merke til at Samtale-Alternativet har ingen verdi opp til aksjekursen treff €40. Ser vi bakover for å Sette Alternativet, hvor verdien null treff når aksjekursen går over €85.,

    Hvis vi forberede det samme følsomhet tabell for Streik Pris, kan vi observere den omvendte forholdet. Som innløsningskurs øker, Ring Verdien går ned, og Sette Verdien går opp.

    La oss også ta en titt på risiko-gratis pris., Som det øker, dette øker også nødvendig pris for avkastning. Senere, dette reduserer verdien av aksjer. Vi ser en direkte sammenheng, som risikofri rente øker, Samtale-Alternativet verdi øker også, mens Put-Opsjon verdien synker den er verdt.

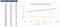
    Etter samme tilnærming, du kan gå videre og se på resten av parametrene og hvordan de påvirker Muligheten Verdier., Du kan laste ned Excel-modell på slutten av artikkelen og gå over sensitivitetsanalyse i det.

    Du kan laste ned eksempel modell i Excel i den opprinnelige artikkelen.

    Konklusjon

    Det er viktig å huske på at Black-Scholes-Merton-modellen er et teoretisk konsept. Vi bruker det for å prøve å anslå atferd i markedet. Imidlertid, når vi bruker resultatene i vår beslutningsprosess, må vi forstå de underliggende forutsetninger i modellen og hvordan den avviker fra virkeligheten.,

    formelen hjalp alternativer handel for å bli mer populære, så det gjør at det ser mindre ut som gambling. I dag, forskjellige modifikasjoner av Black Scholes er allment populær som grunnleggende strategier for risikostyring, knyttet til volatilitet.

    Du kan vise din støtte ved å dele artikkelen med kolleger og venner.