Vektoren sind in der Wissenschaft weitgehend nützlich, um alles zu beschreiben, was sowohl eine Richtung als auch eine Größe hat. Sie werden normalerweise mit Hilfe von spitzen Pfeilen gezeichnet, deren Länge die Größe des Vektors darstellt. Der Pass eines Quarterbacks ist das einfache Beispiel, weil er die Richtung normalerweise irgendwo im Unterfeld und eine Größe hat. Manchmal müssen wir zwei Vektoren zusammen behandeln, die an einem Objekt arbeiten. In solchen Fällen sind Winkel zwischen diesen Vektoren wichtig., In diesem Thema wird der Winkel zwischen zwei Vektoren sowie Beispiele erläutert. Lass es uns lernen!
Konzept der Vektoren
Abseits des Feldes können Vektoren verwendet werden, um eine beliebige Anzahl physikalischer Objekte oder Aktivitäten darzustellen. Beispielsweise. Wind zum Beispiel ist eine vektorielle Größe. Es ist, weil es an jedem gegebenen Ort eine Richtung sowie die Größe hat. Wir können zu jedem Zeitpunkt eine Karte des Luftstroms erstellen, indem wir die Windvektoren für eine Reihe verschiedener geografischer Standorte zeichnen.
Viele Eigenschaften bewegter Objekte sind auch Vektoren., In Billardkugel, sein Geschwindigkeitsvektor beschreibt seine Bewegung. Es zeigt die Richtung der Vektorpfeilmarkierungen als Bewegungsrichtung und die Länge des Vektors stellt die Geschwindigkeit des Balls dar.
Der Impuls der Billardkugel ist auch ein Beispiel für die Vektorgröße. Da es gleich Masse mal Geschwindigkeit ist. Daher ist der Impulsvektor der Kugelpunkte in der gleichen Richtung wie sein Geschwindigkeitsvektor. Und die Größe des Impulsvektors ist das Multiplikationsprodukt aus der Geschwindigkeit des Balls und seiner Masse.,
In Bezug auf Mathematik ist ein Vektor ein beliebiges Objekt mit einer definierbaren Größe und Richtung. Da Vektoren nicht mit Standardlinien oder-formen identisch sind, müssen wir einige spezielle Formeln verwenden, um Winkel zwischen ihnen zu finden.
Die Formel für den Winkel zwischen zwei Vektoren
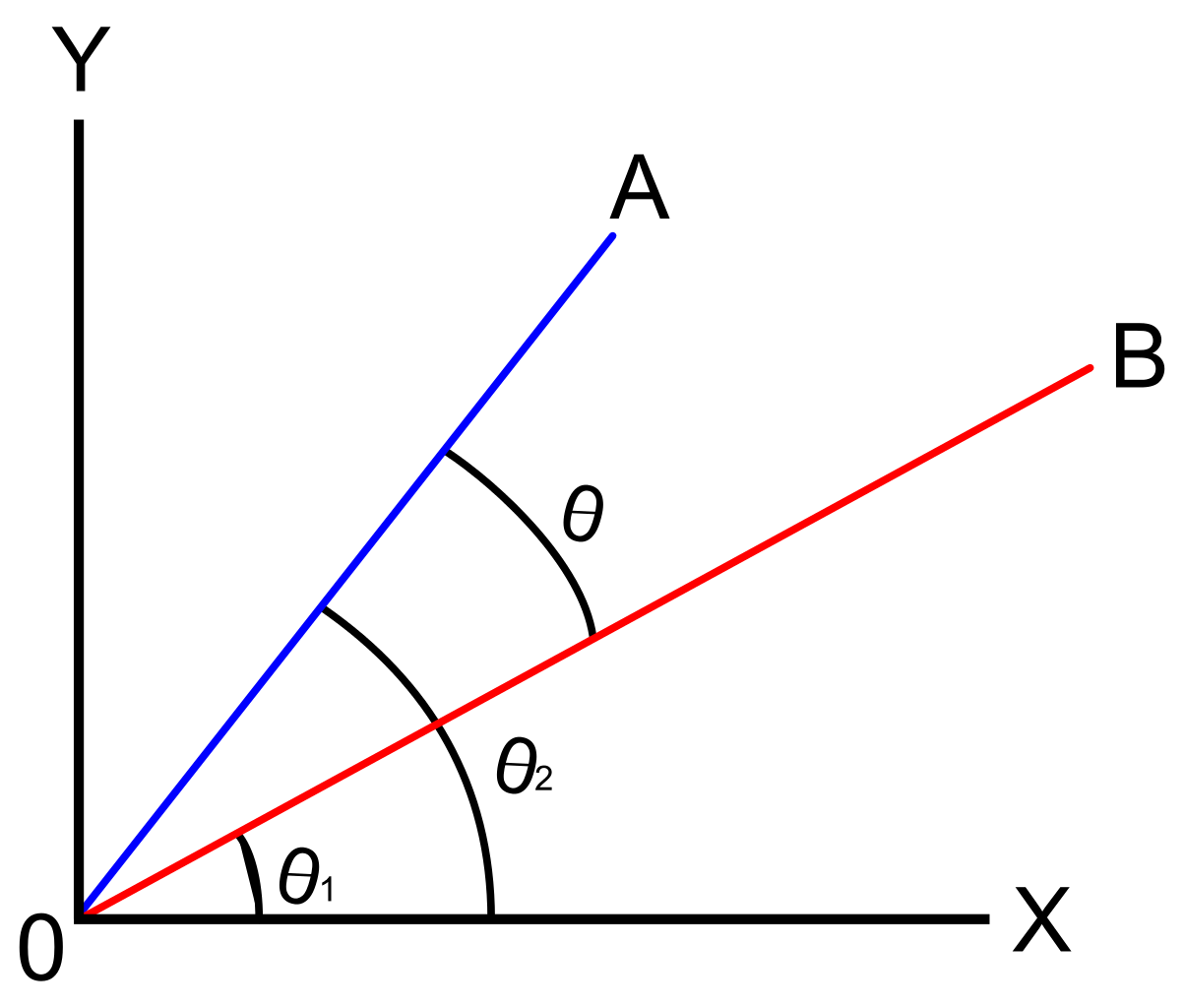
Der Winkel zwischen zwei Vektoren wird um einen einzigen Punkt verschoben, der als der kürzeste Winkel bezeichnet wird, bei dem wir einen der Vektoren an die Position der kodirektionalen mit einem anderen Vektor umdrehen müssen.,
Die Diskussion über Richtungswinkel von Vektoren konzentriert sich auf das Finden des Winkels eines Vektors in Bezug auf die positive x-Achse. Dies konzentriert sich auf den Winkel zwischen zwei Vektoren in der Standardposition. Ein Vektor soll sich in der Standardposition befinden, wenn sein Anfangspunkt der Ursprung (0, 0) ist.
Wenn die beiden Vektoren als a und b angenommen werden, wird der erzeugte Punkt als a definiert .b. Nehmen wir an, diese beiden Vektoren sind durch den Winkel \(\theta\) getrennt. Um zu wissen, was die Winkelmessung ist, werden wir mit Hilfe der gegebenen Formel lösen:
Wir kennen das Punktprodukt:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Jetzt, den Winkel zwischen zwei Vektoren-Formel:
– \(\theta = cos^{-1}\frac{\vec{a}.\vec{b}} {/\vec{a}| / \vec{b}/}\)
Wobei \\(theta\) der Winkel zwischen a-und b-Vektoren ist.
Gelöst Beispiele für Winkel zwischen zwei Vektoren Formel
Q. 1: Berechnen Sie den Winkel zwischen zwei Vektoren 3i + 4j-k und 2i-j + k.
Lösung: Let,
a = 3i + 4j-k und
b = 2i-j + k
Wir definieren das Punktprodukt als:
a.b = (3i + 4j – k).(2i – j + k)
















Schreibe einen Kommentar