Die Chancen stehen gut, dass Sie sich an Erwin Schrödinger (der an diesem Tag vor 128 Jahren geboren wurde) für seine berühmte Katze erinnern, aber der Höhepunkt der Karriere des gefeierten Physikers hatte eigentlich nichts mit katzenartigen Gedankenexperimenten zu tun. Unter Wissenschaftlern ist er dafür bekannt, uns die grundlegenden Werkzeuge zur Beschreibung des Quantenverhaltens zu geben.,

Eine Sprache für das Studium der Quantenwelt schaffen

Die 1920er Jahre, in denen die Quantenmechanik—die Funktionsweise der kleinsten und grundlegendsten Bestandteile aller Materie—geboren wurde, waren eine aufregende Zeit, um Physiker zu sein. Die größten lebenden Köpfe beeilten sich, Wege zu finden, diese neue Welt zu beschreiben, die aufgerissen worden war. Werner Heisenberg entwickelte seine Formulierung der Quantenmechanik mit Matrizen, einem System, das nur Algebra erforderte. Aber Schrödinger dachte an ein anderes Modell mit Wellen anstelle von Matrizen.,

Die Wellenfunktionen von Schrödingers Modell, sagt der Physiker Sean Carroll ,“ sind schwieriger zu lösen, aber intuitiver.“

Schrödingers Modell beruht auf seiner gleichnamigen Gleichung, die die Entwicklung der Wellenfunktion eines physikalischen Systems im Laufe der Zeit beschreibt. Es ist irgendwie wie eine Quantenversion von Newtons zweitem Bewegungsgesetz (Kraft = Masse x Beschleunigung). Bei der Beschreibung des Verhaltens von Teilchen funktionieren Newtons Regeln nicht so gut, daher muss die Mathematik etwas komplexer werden., Hier ist die allgemeinste Form der Gleichung:

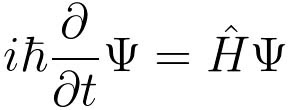In dieser Formel ist i die imaginäre Einheit (die Quadratwurzel von -1); ħ steht für die Planck-Konstante geteilt durch 2π; ∂/∂t ist eine partielle Ableitung, die sich im Laufe der Zeit ändert; Ψ ist die Wellenfunktion des Systems; und Ĥ ist der Hamilton-Operator, der die Energie des Systems darstellt. Der hamiltonsche Operator ist der Schlüsselteil: Er beschreibt die Art von System, die wir betrachten.,

„Schrodingers Gleichung liegt im Herzen der theoretischen Physik“, sagt Brian Greene, Mitbegründer des World Science Festival und Physiker der Columbia University. Die Gleichung “ ist keine einzige mathematische Aussage. Es ist eine allgemeine Beziehung, die, soweit wir wissen, immer gilt. In jeder Situation müssen Sie wissen, wie Sie diese Beziehung anwenden, und die Details dieser Anwendung variieren von Situation zu Situation. Aber das Gesetz ist, soweit wir wissen, ein Gesetz.,“

Zurück zu den Besonderheiten der Formel: Setzen Sie alles zusammen und wenn Sie zu einem bestimmten Zeitpunkt eine Momentaufnahme der „Welle“ haben, können Sie mit Schrödingers Gleichung darüber sprechen, wie sie in Zukunft aussehen wird.

„Ich denke an alle Gleichungen, die wir derzeit kennen, wird höchstwahrscheinlich in 1.000 Jahren halten“, sagt Carroll.

Eine bahnbrechende Gleichung, die zu einem Nobelpreis führte

Diese Formel war zu dieser Zeit eine Offenbarung., Es erklärt die Tatsache, dass sich Partikel normalerweise nicht wie kleine Billardkugeln verhalten, die über einen Tisch gleiten; Manchmal werden sie besser als Wellen angesehen. Während der französische Physiker Louis de Broglie bereits vermutet hatte, dass es eine Welle-Teilchen-Dualität gibt, erlaubte Schrödinger den Wissenschaftlern, Teilchen—und ihre damit verbundenen Wellen—in Aktion zu beschreiben. Das war eine beeindruckende Leistung für die Wissenschaftler, die im Nobelpreiskomitee saßen und Schrödinger 1933 einen Nobelpreis für Physik verlieh (gemeinsam mit dem Wellenmechaniker Paul Dirac).,

„Durch eine Untersuchung der Welleneigenschaften der Materie ist es gelungen, ein neues System der Mechanik zu etablieren, das auch für die Bewegung innerhalb der Atome und Moleküle gut ist“, sagte H. Pleijel, damals Vorsitzender des Nobelkomitees für Physik, in einer Rede von 1933, in der die diesjährigen Preise vorgestellt wurden. „Schrödingers Wellengleichung hat eine bequeme und einfache Methode zur Behandlung von Problemen mit Lichtspektren zur Verfügung gestellt und ist zu einem unverzichtbaren Werkzeug für den heutigen Physiker geworden.“

Zurück zur Katze

Und als Coda (natürlich lateinisch für Schwanz) kehren wir schnell zur Katze zurück., Obwohl es nicht ganz so unverzichtbar ist wie Schrödingers Gleichung, schwingt das Gedankenexperiment „Schrödingers Katze“ immer noch als kraftvolle Illustration der Quecksilbernatur der Quantenmechanik mit. Für eine Auffrischung auf genau das, was es bedeutet, Besuche dieses Video von Brian Greene.