Wenn sich die Winkel eines Dreiecks nicht zu 180 Grad addieren

1. Einleitung

Addieren sich die Winkel eines Dreiecks zu 180 Grad oder$ \pi $ Radiant? Die Antwort lautet „manchmal ja, manchmal nein“. Ist das eine wichtige Frage? Ja, weil es zu einem Verständnis führt, dass es verschiedene Geometrien gibt, die auf verschiedenen Axiomen oder „Regeln des Geometriespiels“ basieren. Ist es eine sinnvolle Frage? Nun nein, zumindest nicht, bis wir uns auf die Bedeutung der Wörter „Winkel“ und „Winkel“ geeinigt haben, nicht, bis wir die Spielregeln kennen., In diesem Artikel diskutieren wir kurz die zugrunde liegenden Axiome und geben einen einfachen Beweis dafür, dass die Summe der Winkel eines Dreiecks auf der Oberfläche einer Einheitskugel nicht gleich $\pi$, sondern $\pi$ plus der Fläche des Dreiecks ist. Wir werden die Tatsache verwenden, dass die Fläche der Oberfläche einer Einheitskugel $4\pi$beträgt.

2. Der große Satz

Bevor wir sagen können, was ein Dreieck ist, müssen wir uns darauf einigen, was wir mit Punkten und Linien meinen. Wir arbeiten an sphärischer Geometrie (wörtlich Geometrie auf der Oberfläche einer Kugel)., In dieser Geometrie ist der Raum die Oberfläche der Kugel; Die Punkte sind Punkte auf dieser Oberfläche, und die Linie des kürzesten Abstandes zwischen zwei Punkten ist der große Kreis, der die beiden Punkte enthält. Ein großer Kreis (wieder Äquator) schneidet die Kugel in zwei gleiche Hemisphären. Diese Geometrie hat offensichtliche Anwendungen auf Entfernungen zwischen Orten und Flugrouten auf der Erde.,

Rotierende Kugel mit großem Kreis

Der Winkel zwischen zwei großen Kreisen an einem Punkt P ist der euklidische Winkel zwischen den Richtungen der Kreise (oder genau zwischen den Tangenten zu den Kreisen bei P). Dies stellt keine Schwierigkeiten bei der Navigation auf der Erde dar, da wir an einem bestimmten Punkt den Winkel zwischen zwei Richtungen betrachten, als wäre die Erde an diesem Punkt flach.

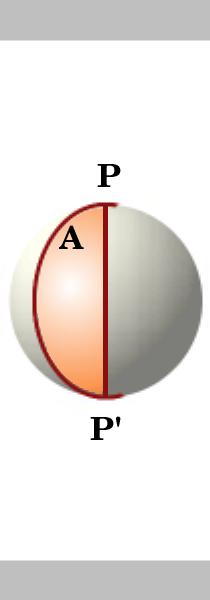
Eine Lune ist ein Teil der Oberfläche der Kugel, der von zwei großen Kreisen begrenzt wird, die sich an antipodalen Punkten treffen., Wir betrachten zuerst die Fläche einer Lune und führen dann einen weiteren großen Kreis ein, der die Lune in Dreiecke aufteilt.

Rotierende Kugel zeigt 4 Montag –

Lemma.

Die Fläche eines Lune auf einem Kreis mit Einheitsradius ist doppelt so groß wie sein Winkel, dh wenn der Winkel des Lune A ist, dann ist seine Fläche 2A. Zwei große Kreise, die sich an den antipodalen Punkten P und P schneiden, teilen die Kugel in 4 Lune. Die Fläche der Oberfläche einer Einheitskugel beträgt $4\pi$.,

Die Flächen der Lune sind proportional zu ihren Winkeln bei P, so dass die Fläche einer Lune mit Winkel A

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Übung 1.

Was sind die Bereiche der anderen 3 lunes? Addieren sich Ihre 4 Bereiche zu $4\pi$?

Überprüfen Sie Ihre Antworten hier .

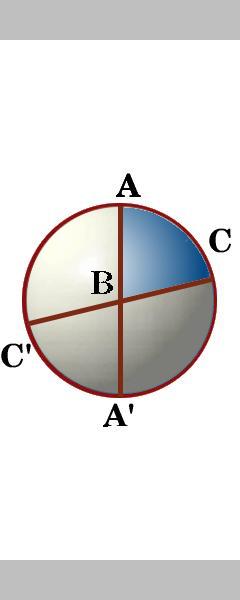
Die Seiten eines Dreiecks ABC sind Segmente von drei großen Kreisen, die die Oberfläche der Kugel tatsächlich in acht kugelförmige Dreiecke schneiden. Zwischen den beiden großen Kreisen durch den Punkt A gibt es vier Winkel., Wir bezeichnen den Winkel innerhalb des Dreiecks ABC als Winkel A und in ähnlicher Weise die anderen Winkel des Dreiecks ABC als Winkel B und Winkel C.

Rotierende Kugel mit 8 Dreiecken

Übung 2

Drehen der Kugel Können Sie die acht Dreiecke benennen und sagen, ob eines von ihnen dieselbe Fläche hat? Überprüfen Sie Ihre Antworten hier .

– Theorem.

Betrachten Sie ein kugelförmiges Dreieck ABC auf der Einheitskugel mit den Winkeln A, B und C. Dann ist die Fläche des Dreiecks ABC

A + B + C – $\pi$.,

Das Diagramm zeigt eine Ansicht nach unten auf der Hemisphäre, die die Linie durch AC als Grenze hat. Die mit Bereich 1 und Bereich 3 gekennzeichneten Bereiche sind Lunes mit den Winkeln A bzw. Betrachten Sie die Lunes durch B und B‘. Das Dreieck ABC ist kongruent zum Dreieck A ‚ B ‚C‘, so dass der bogenförmige schattierte Bereich, markierter Bereich 2, der die Summe der Bereiche der Dreiecke ABC und A‘ BC ‚ ist, gleich diearea der Lune mit Winkel B, das ist gleich 2B.,

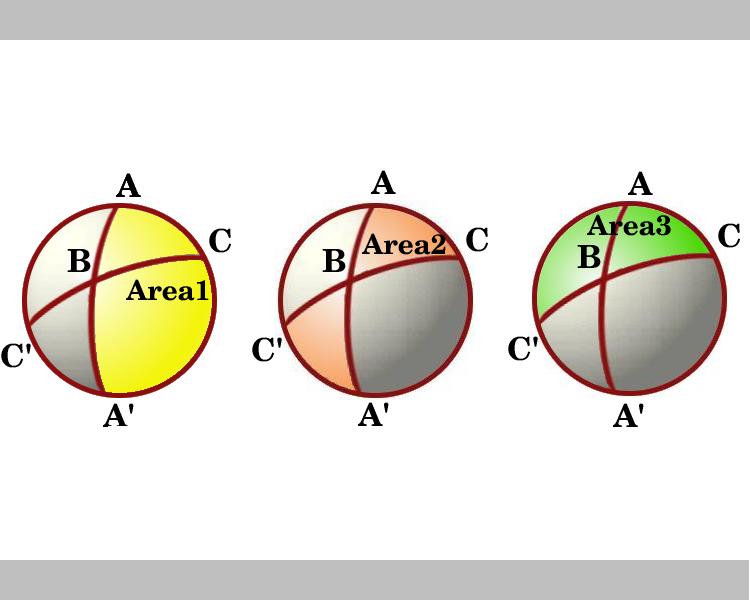
Im Diagramm sehen wir also die Bereiche von drei Lunes und unter Verwendung des Lemmas sind dies:

Bereich 1 = 2A
Bereich 2 = 2B
Bereich 3 = 2C

Wenn wir diese drei Bereiche addieren, fügen wir dreimal die Fläche des Dreiecks ABC hinzu., Hence

3., Nicht-euklidische Geometrie

Manchmal sind revolutionäre Entdeckungen nichts anderes, als tatsächlich zu sehen, was die ganze Zeit unter unserer Nase war. Dies war der Fall über die Entdeckung der nicht-euklidischen Geometrie im neunzehnten Jahrhundert. Seit ungefähr 2000 Jahren, nachdem Euklid seine „Elemente“ in 325 BC geschrieben hatte, versuchten die Leute, das parallele Postulat als Theorem in der Geometrie von den anderen Axiomen zu beweisen, scheiterten aber immer und das ist eine lange Geschichte., In der Zwischenzeit verwendeten Mathematiker die sphärische Geometrie die ganze Zeit, eine Geometrie, die den anderen Axiomen der euklidischen Geometrie gehorcht und viele der gleichen Theoreme enthält, in denen das parallele Postulat jedoch nicht gilt. Die ganze Zeit hatten sie ein Beispiel für eine nicht-euklidische Geometrie unter der Nase.

Denken Sie an eine Linie L und einen Punkt P nicht auf L. Die große Frage ist: „Wie viele Linien können parallel zu L durch P gezogen werden?“In der euklidischen Geometrie lautet die Antwort `genau eins“ und dies ist eine Version des parallelen Postulats., Wenn die Summe der Winkel jedes Dreiecks in der Geometrie $ \ pi$ Radiant ist, dann gilt das parallele Postulat und umgekehrt, die beiden Eigenschaften sind äquivalent.

In der sphärischen Geometrie unterscheiden sich die grundlegenden Axiome, die wir annehmen (die Spielregeln), von der euklidischen Geometrie – dies ist eine nicht-euklidische Geometrie. Wir haben gesehen, dass in der sphärischen Geometrie die Winkel von Dreiecken nicht immer $\pi$ Radiant addieren, so dass wir nicht erwarten würden, dass das parallele Postulat gilt., In der sphärischen Geometrie sind die geraden Linien (Linien kürzester Entfernung oder Geodäsie)große Kreise und jede Linie in der Geometrie schneidet jede andere Linie in zwei Punkte. Die Antwort auf die große Frage nach Parallelen lautet` “ Wenn wir eine Linie L und einen Punkt P nicht auf L haben, gibt es keine Linien durch P parallel zur Linie L.,“

Die griechischen Mathematiker (zum Beispiel Ptolemäus c 150) berechneten die Messungen rechtwinkliger sphärischer Dreiecke und arbeiteten mit Formeln der sphärischen Trigonometrie und arabische Mathematiker (zum Beispiel Jabir ibn Aflah c 1125 und Nasir ed-din c 1250) erweiterten die Arbeit noch weiter. Die in diesem Artikel diskutierte Formel wurde 1603 von Harriot entdeckt und 1629 von Girard veröffentlicht. Weitere Themen des Themas wurden von Saccerhi (1667 – 1733) entwickelt.,Jahrhundert Entdeckern der hyperbolischen Geometrie, die eine andere nicht-euklidische Geometrie ist, in der das parallele Postulat nicht gilt, weitgehend unbeachtet. In der sphärischen Geometrie (auch elliptische Geometrie genannt) summieren sich die Winkel von Dreiecken zu mehr als $\pi$ Radiant und in der hyperbolischen Geometrie summieren sich die Winkel von Dreiecken zu weniger als $\pi$ Radiant.

Weitere Informationen finden Sie im Artikel von Alan Beardon ‚ Wie viele Geometrien gibt es?’und der Artikel von Keith Carne ‚Seltsame Geometrien‘., Es gibt einige praktische Aktivitäten, die Sie selbst ausprobieren können, um diese Geometrien weiter zu erforschen http://nrich.maths.org/MOTIVATE/conf8/index.html