Wahrscheinlichkeit für das Würfeln von zwei Würfeln mit den sechsseitigen Punkten wie 1, 2, 3, 4, 5 und 6 Punkte in jedem Würfel.

Wenn zwei Würfel gleichzeitig geworfen werden, kann die Anzahl der Ereignisse 62 = 36 sein, da jeder Würfel 1 bis 6 hat Zahl auf seinen Gesichtern. Dann werden die möglichen Ergebnisse in der folgenden Tabelle gezeigt.,
Wahrscheinlichkeit-Beispielraum für zwei Würfel (Ergebnisse):
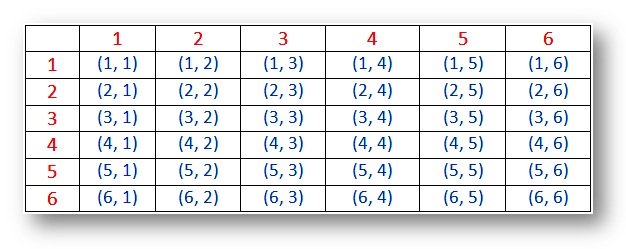
Hinweis:
(i) Die Ergebnisse sind(1, 1), (2, 2), (3, 3), (4, 4), (5, 5) und (6, 6) werden Doublets genannt.
(ii) Das paar (1, 2) und (2, 1) sind unterschiedliche Ergebnisse.
Ausgearbeitete Probleme mit Wahrscheinlichkeit für das Würfeln von zwei Würfeln:
1. Zwei Würfel werden gerollt. Sei A, B, C die Ereignisse, um eine Summe von 2, eine Summe von 3 und eine Summe von 4 zu erhalten., Zeigen Sie dann, dass
(i) A ein einfaches Ereignis ist
(ii) B und C sind zusammengesetzte Ereignisse
(iii) A und B schließen sich gegenseitig aus
Lösung:
Klar, wir haben
A = {(1, 1)}, B = {(1, 2), (2, 1)} und C = {(1, 3), (3, 1), (2, 2)}.
(i) Da A aus einem einzelnen Beispielpunkt besteht, ist es ein einfaches Ereignis.
(ii) Da sowohl B als auch C mehr als einen Probenpunkt enthalten, ist jeder von ihnen ein zusammengesetztes Ereignis.
(iii) Da A ∩ B = ∅, A und B schließen sich gegenseitig aus.
2. Zwei Würfel werden gerollt., A ist das Ereignis, dass die Summe der Zahlen auf den beiden Würfeln gezeigt ist 5, und B ist das Ereignis, dass mindestens einer der Würfel zeigt eine 3.
Schließen sich die beiden Ereignisse (i) gegenseitig aus, (ii) erschöpfend? Geben Sie Argumente zur Unterstützung Ihrer Antwort.
Lösung:
Wenn zwei Würfel gerollt werden, haben wir n(S) = (6 × 6) = 36.
Jetzt, EIN = {(1, 4), (2, 3), (4, 1), (3, 2)}, und
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
Daher schließen sich A und B nicht gegenseitig aus.,
(ii) Auch A ∪ B ≠ S.
Daher sind A und B keine erschöpfenden Ereignisse.
Weitere Beispiele zu den Fragen zu den Wahrscheinlichkeiten für das Werfen von zwei Würfeln.
3. Zwei Würfel werden gleichzeitig geworfen.,) getting a doublet
(v) getting a sum of 8
(vi) getting sum divisible by 5
(vii) getting sum of atleast 11
(viii) getting a multiple of 3 as the sum
(ix) getting a total of atleast 10
(x) getting an even number as the sum
(xi) erhalten einer Primzahl als Summe
(xii) Erhalten eines Doublets gerader Zahlen
(xiii) Erhalten eines Vielfachen von 2 auf einem Würfel und eines Vielfachen von 3 auf dem anderen Würfel
Lösung:
Zwei verschiedene Würfel werden gleichzeitig geworfen und sind die Nummern 1, 2, 3, 4, 5 und 6 auf ihren Gesichtern., Wir wissen, dass in einem einzigen Wurf von zwei verschiedenen Würfeln, die Gesamtzahl der möglichen Ergebnisse ist (6 × 6) = 36.
(ich) immer sechs als Produkt:
Lassen E1 = event zu bekommen, sechs wie ein Produkt. Die Zahl, deren Produkt sechs ist, ist E1 = = 4
Daher Wahrscheinlichkeit, „sechs als Produkt“ zu setzen
Anzahl günstiger Ergebnisse
P (E1) = Gesamtzahl möglicher Ergebnisse
= 4/36
= 1/9
(ii) Summe ≤ 3 erhalten:
Sei E2 = Ereignis, Summe ≤ 3 zu erhalten., Die Zahl, deren Summe ≤ 3 E2 = = 3
sein wird, ist daher Wahrscheinlichsetzensumme ≤ 3 ‚
Anzahl günstiger Ergebnisse
P (E2) = Gesamtzahl möglicher Ergebnisse
= 3/36
= 1/12
(iii) Summe ≤ 10 erhalten:
Sei E3 = Ereignis, Summe ≤ 10 zu erhalten. Die Zahl, deren Summe ≤ 10 E3 =
= 33
sein wird, ist daher Wahrscheinlichsetzen von ‚Summe ≤ 10‘
Anzahl günstiger Ergebnisse
P (E3) = Gesamtzahl möglicher Ergebnisse
= 33/36
= 11/12
(iv) Erhalten eines Doublets:Sei E4 = Ereignis, ein Doublet zu erhalten., Die Anzahl der Wams wird E4 = = 6
Daher, die Wahrscheinlichkeit, ofgetting ‚ein Dublett‘
Anzahl der günstigen Ergebnisse
P(E4) = Anzahl der möglichen Ergebnisse
= 6/36
= 1/6
(v)immer eine Summe von 8:
Lassen E5 = event immer eine Summe von 8. Die Reihe ist eine Summe von 8 E5 = = 5
Daher, die Wahrscheinlichkeit, ofgetting ‚eine Summe von 8‘
Anzahl der günstigen Ergebnisse
P(E5) = Anzahl der möglichen Ergebnisse
= 5/36
, (vi)die erste Summe teilbar durch 5:
Lassen E6 = event zu bekommen Summe teilbar durch 5., Die Zahl, deren Summe durch 5 teilbar wird E6 = = 7
Daher Wahrscheinlichkeit ofgetting ‚Summe durch 5 teilbar‘
Anzahl der günstigen Ergebnisse
P (E6) = Gesamtzahl der möglichen Ergebnis
= 7/36
(vii) getting Summe von atleast 11:
Let E7 = Ereignis getting Summe von atleast 11. Die Ereignisse der Summe mindestens 11 E7 = = 3
Daher, die Wahrscheinlichkeit, ofgetting ‚die Summe von mindestens 11‘
Anzahl der günstigen Ergebnisse
P(E7) = Anzahl der möglichen Ergebnisse
= 3/36
= 1/12
(viii) erste amultiple 3 als Summe:
Lassen E8 = event immer ein Vielfaches von 3 als die Summe., Die Ereignisse der ein Vielfaches von 3 als die Summe wird E8 = = 12
Daher, die Wahrscheinlichkeit, ofgetting ‚ein Vielfaches von 3 als die Summe‘
Anzahl der günstigen Ergebnisse
P(E8) = Anzahl der möglichen Ergebnisse
= 12/36
= 1/3
(ix) immer eine insgesamt atleast 10:
Lassen E9 = event zu bekommen, insgesamt mindestens 10., Die Veranstaltungen von insgesamt mindestens 10 E9 = = 6
Daher, die Wahrscheinlichkeit, ofgetting ‚insgesamt mindestens 10‘
Anzahl der günstigen Ergebnisse
P(E9) = Anzahl der möglichen Ergebnisse
= 6/36
= 1/6
(x) immer eine evennumber als die Summe:
Lassen E10 = – Ereignis immer eine gerade Zahl als Summe., Die Ereignisse einer geraden Zahl als Summe sind E10 = = 18
Daher Wahrscheinlichkeit, eine gerade Zahl als Summe zu setzen
Anzahl günstiger Ergebnisse
P (E10) = Gesamtzahl möglicher Ergebnisse
= 18/36
= 1/2
(xi) Erhalten einer Primzahl als Summe:
Lassen Sie E11 = Ereignis, eine Primzahl als Summe zu erhalten., Die Ereignisse einer Primzahl als Summe sind E11 = = 15
Daher Wahrscheinlichkeit, eine Primzahl als Summe zu setzen
Anzahl günstiger Ergebnisse
P (E11) = Gesamtzahl möglicher Ergebnisse
= 15/36
= 5/12
(xii) Adoublet gerader Zahlen erhalten:
Let E12 = Ereignis, ein Doublet gerader Zahlen zu erhalten., Die Ereignisse eines Doublets von geraden Zahlen sind E12 = = 3
Daher Wahrscheinlichkeit, ein Doublet von geraden Zahlen zu setzen
Anzahl der günstigen Ergebnisse
P(E12) = Gesamtzahl der möglichen Ergebnisse
= 3/36
= 1/12
(xiii) Erhalten Sie ein Vielfaches von 2 auf einem Würfel und ein Vielfaches von 3 auf dem anderen Würfel:
Lassen Sie E13 = Ereignis, ein Vielfaches von 2 auf einem Würfel und vielfaches von 3 auf der anderen sterben., Die Ereignisse eines vielfachen von 2 auf einem Würfel und eines Vielfachen von 3 auf dem anderen Würfel sind E13 = = 11
Daher Wahrscheinlichkeit ofgetting ‚ein Vielfaches von 2 auf einem Würfel und ein Vielfaches von 3 auf dem anderen Würfel‘
Anzahl der günstigen Ergebnisse
P(E13) = Gesamtzahl der möglichen Ergebnisse
= 11/36
4. Zwei werden geworfen. Finden Sie (i) die Chancen, die Summe 5 zu erhalten, und (ii) die Chancen, die Summe 6 zu erhalten.
Lösung:
Wir wissen, dass in einem einzigen Wurf von zwei Würfel, die Gesamtzahl der möglichen Ergebnisse ist (6 × 6) = 36.
Sei S der Sample Space. Dann ist n (S) = 36.,
(i) die Chancen, die Summe 5 zu erhalten:
Sei E1 das Ereignis, die Summe 5 zu erhalten. Dann,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Daher P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ Quoten zugunsten von E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) die Chancen, die Summe 6 zu erhalten:
Sei E2 das Ereignis, die Summe 6 zu erhalten. Dann,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Daher P(E2) = n(E2)/n(S) = 5/36
⇒ Quoten gegen E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Zwei Würfel, ein blau und ein orange, werden gleichzeitig gerollt. Finden Sie die Wahrscheinlichkeit,
zu erhalten (i) gleiche Zahlen für beide
(ii) zwei Zahlen, deren Summe 9 ist.,
Lösung:
Die möglichen Ergebnisse sind
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
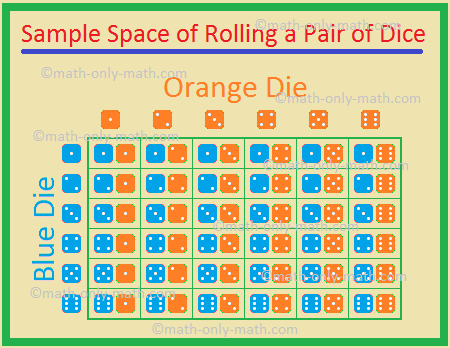
Daher Gesamtzahl der möglichen Ergebnisse = 36.,
(i) Anzahl der positiven Ergebnisse für das Ereignis E
= Anzahl der Ergebnisse mit gleicher Anzahl auf beiden Würfeln
= 6 .
Also per Definition P (E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Anzahl der positiven Ergebnisse für das Ereignis F
= Anzahl der Ergebnisse, bei denen zwei Zahlen auf ihnen die Summe 9
= 4 haben .
Also, per definition, dass P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
Diese Beispiele helfen Ihnen, verschiedene Arten von Problemen zu lösen, basierend auf der Wahrscheinlichkeit, zwei Würfel zu würfeln.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Schreibe einen Kommentar