Show Mobile Bemerken, Zeigen Sie Alle Notizen Ausblenden, Alle Notizen
Abschnitt 3-1: Parametrische Gleichungen und Kurven
Bis zu diesem Punkt(sowohl in Kalkül I als auch in Kalkül II) haben wir uns fast ausschließlich Funktionen in der Form angesehen \(y = f\left(x \right)\) oder \(x = h\left (y \right)\) und fast alle Formeln, die wir entwickelt haben, erfordern, dass Funktionen in einer dieser beiden Formen vorliegen. Das Problem ist, dass nicht alle Kurven oder Gleichungen, die wir betrachten möchten, leicht in diese Form fallen.
Nehmen Sie zum Beispiel einen Kreis. Es ist leicht genug, die Gleichung eines Kreises, der am Ursprung zentriert ist, mit Radius \(r\) aufzuschreiben.,
\
Wir werden jedoch niemals in der Lage sein, die Gleichung eines Kreises als eine einzige Gleichung in einer der oben genannten Formen aufzuschreiben. Sicher können wir für \(x\) oder \(y\) lösen, da die folgenden zwei Formeln
\
aber es gibt tatsächlich zwei Funktionen in jeder von diesen. Jede Formel gibt einen Teil des Kreises an.
\
Leider arbeiten wir normalerweise am ganzen Kreis oder können einfach nicht sagen, dass wir nur an einem Teil davon arbeiten werden. Auch wenn wir die Dinge auf nur einen dieser Teile eingrenzen können, ist die Funktion oft noch ziemlich unangenehm zu arbeiten.,
\
Diese dritte Variable wird normalerweise mit \(t\) bezeichnet (wie wir es hier getan haben), muss aber natürlich nicht sein. Manchmal beschränken wir die Werte von \(t\), das wir verwenden werden, und zu anderen Zeiten nicht. Dies wird oft davon abhängig sein, das problem und das was wir gerade versuchen zu tun.
Um zu visualisieren, was eine parametrische Kurve ist, tun Sie so, als hätten wir einen großen Wassertank, der sich in ständiger Bewegung befindet, und lassen Sie einen Tischtennisball in den Tank fallen., Der Punkt \(\left ({x,y} \right) = \left ({f\left( t \right),g\left(t \right)} \right)\) repräsentiert dann die Position des Tischtennisballs im Tank zum Zeitpunkt \(t\) und die parametrische Kurve ist eine Spur aller Positionen des Tischtennisballs. Beachten Sie, dass dies nicht immer eine korrekte Analogie ist, aber es ist zunächst nützlich, um zu visualisieren, was eine parametrische Kurve ist.
Das Skizzieren einer parametrischen Kurve ist nicht immer einfach. Schauen wir uns ein Beispiel an, um eine Möglichkeit zum Skizzieren einer parametrischen Kurve zu sehen., Dieses Beispiel zeigt auch, warum diese Methode normalerweise nicht die beste ist.
An dieser Stelle besteht unsere einzige Option zum Skizzieren einer parametrischen Kurve darin, Werte von \(t\) auszuwählen, sie in die parametrischen Gleichungen einzufügen und dann die Punkte zu zeichnen. Also, lassen sie uns stecker in einige \(t\)’s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Leider gibt es zu diesem Zeitpunkt keine wirkliche Antwort auf diese Frage. Wir wählen einfach \(t\), bis wir ziemlich sicher sind, dass wir eine gute Vorstellung davon haben, wie die Kurve aussieht. Es ist dieses Problem mit der Auswahl von“ guten “ Werten von \(t\), das diese Methode zum Skizzieren parametrischer Kurven zu einer der schlechteren Entscheidungen macht. Manchmal haben wir keine Wahl, aber wenn wir eine Wahl haben, sollten wir es vermeiden.
Wir werden eine alternative Grafikmethode in späteren Beispielen diskutieren, die helfen zu erklären, wie diese Werte von \(t\) ausgewählt wurden.,
Wir haben noch eine Idee zu besprechen, bevor wir die Kurve tatsächlich skizzieren. Parametrische Kurven haben eine Bewegungsrichtung. Die Bewegungsrichtung ist durch Erhöhen von \(t\) gegeben. Wenn wir also parametrische Kurven zeichnen, fügen wir auch Pfeile hinzu, die die Bewegungsrichtung anzeigen. Wir geben oft den Wert von \(t\) an, der auch bestimmte Punkte im Diagramm angegeben hat, um den Wert von \(t\) zu verdeutlichen, der diesen bestimmten Punkt angegeben hat.
Hier ist die Skizze dieser parametrischen Kurve.
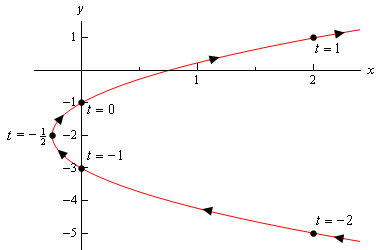
Es sieht also so aus, als hätten wir eine Parabel, die sich nach rechts öffnet.,
Bevor wir dieses Beispiel beenden, gibt es einen etwas wichtigen und subtilen Punkt, den wir zuerst diskutieren müssen. Beachten Sie, dass wir darauf geachtet haben, einen Teil der Skizze rechts von den Punkten hinzuzufügen, die \(t = – 2\) und \(t = 1\) entsprechen, um anzuzeigen, dass Teile der Skizze vorhanden sind. Hätten wir die Skizze einfach an diesen Punkten angehalten, zeigen wir an, dass sich rechts von diesen Punkten kein Teil der Kurve befand und dies eindeutig der Fall sein wird. Wir haben einfach keinen dieser Punkte berechnet.,
Dies mag ein unwichtiger Punkt sein, aber wie wir im nächsten Beispiel sehen werden, ist es wichtiger als wir vielleicht denken.
Bevor wir uns mit einem viel einfacheren Weg befassen, um dieses Diagramm zu skizzieren, wollen wir uns zunächst mit dem Problem der Grenzen des Parameters befassen. Im vorherigen Beispiel hatten wir keine Grenzen für den Parameter. Ohne Begrenzung des Parameters wird das Diagramm in beide Richtungen fortgesetzt, wie in der obigen Skizze gezeigt.
Wir werden jedoch häufig Grenzen für den Parameter haben, was sich auf die Skizze der parametrischen Gleichungen auswirkt., Um diesen Effekt zu sehen, schauen wir uns eine leichte Variation des vorherigen Beispiels an.
Beachten Sie, dass der einzige Unterschied hier das Vorhandensein der Grenzen für \(t\) ist. All diese Grenzen sagen uns, dass wir keinen Wert von \(t\) außerhalb dieses Bereichs annehmen können. Daher ist die parametrische Kurve nur ein Teil der obigen Kurve. Hier ist die parametrische Kurve für dieses Beispiel.,
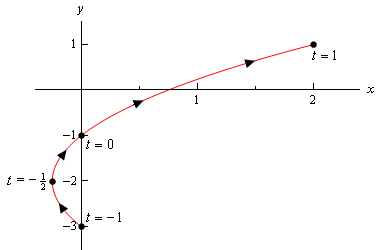
Beachten Sie, dass wir mit dieser Skizze die Skizze direkt an den Punkten gestartet und gestoppt haben, die von den Endpunkten des Bereichs von \(t\) stammen. Kontrastieren Sie dies mit der Skizze im vorherigen Beispiel, in der wir einen Teil der Skizze rechts von den von uns berechneten“ Start „- und“ End “ – Punkten hatten.
In diesem Fall beginnt die Kurve bei \(t = – 1\) und endet bei \(t = 1\), während im vorherigen Beispiel die Kurve nicht wirklich an den von uns berechneten rechten Punkten begann., Wir müssen in unseren Skizzen klarstellen, ob die Kurve direkt an einem Punkt beginnt/endet oder ob dieser Punkt einfach der erste/letzte war, den wir berechnet haben.
Es ist jetzt an der Zeit, einen Blick auf eine einfachere Methode zum Skizzieren dieser parametrischen Kurve zu werfen. Diese Methode verwendet die Tatsache, dass wir in vielen, aber nicht allen Fällen den Parameter tatsächlich aus den parametrischen Gleichungen entfernen und eine Funktion erhalten können, die nur \(x\) und \(y\). Wir werden dies manchmal die algebraische Gleichung nennen, um sie von den ursprünglichen parametrischen Gleichungen zu unterscheiden., Es wird zwei kleine Probleme mit dieser Methode geben, aber es wird leicht sein, diese Probleme anzugehen. Es ist jedoch wichtig zu beachten, dass wir dies nicht immer tun können.
Wie wir den Parameter eliminieren, hängt von den parametrischen Gleichungen ab, die wir haben. Mal sehen, wie der Parameter für den Satz parametrischer Gleichungen, mit denen wir bis jetzt gearbeitet haben, eliminiert wird.
Eine Skizze der parametrischen Kurve zu erhalten, sobald wir den Parameter eliminiert haben, scheint ziemlich einfach zu sein. Alles, was wir tun müssen, ist die Gleichung grafisch darzustellen, die wir durch Eliminieren des Parameters gefunden haben., Wie bereits erwähnt, gibt es jedoch zwei kleine Probleme mit dieser Methode. Die erste ist Bewegungsrichtung. Die Gleichung, die nur \(x\) und \(y\) enthält, gibt NICHT die Bewegungsrichtung der parametrischen Kurve an. Dies ist jedoch im Allgemeinen ein leicht zu behebendes Problem. Werfen wir einen kurzen Blick auf die Ableitungen der parametrischen Gleichungen aus dem letzten Beispiel. Sie sind,
\
Beachten Sie, dass die \(x\) – Ableitung für diese Analyse nicht so nützlich ist, da sie sowohl positiv als auch negativ ist und daher \(x\) je nach Wert von \(t\) sowohl zunimmt als auch abnimmt., Das hilft bei der Richtung nicht viel, da das Folgen der Kurve in beide Richtungen sowohl zunehmendes als auch abnehmendes \(x\) zeigt.
In einigen Fällen gibt nur eine der Gleichungen, wie dieses Beispiel, die Richtung an, während in anderen Fällen eine der beiden verwendet werden könnte. Es ist auch möglich, dass in einigen Fällen beide Derivate benötigt würden, um die Richtung zu bestimmen. Es wird immer von der individuellen Menge parametrischer Gleichungen abhängen.,
Das zweite Problem mit der Beseitigung des Parameters wird am besten in einem Beispiel veranschaulicht, da wir in den verbleibenden Beispielen auf dieses Problem stoßen werden.
Okay, das war ein wirklich langes Beispiel. Die meisten dieser Arten von Problemen sind nicht so lang. Wir hatten gerade viel zu besprechen, damit wir ein paar wichtige Ideen aus dem Weg räumen konnten. Der Rest der Beispiele in diesem Abschnitt sollte nicht so lange dauern.
Schauen wir uns nun ein anderes Beispiel an, das eine wichtige Idee zu parametrischen Gleichungen veranschaulicht.,
Wir haben also in den letzten beiden Beispielen zwei Sätze parametrischer Gleichungen gesehen, die in gewisser Weise dasselbe Diagramm ergeben haben. Da sie den Graphen jedoch unterschiedlich oft nachverfolgt haben, müssen wir sie zumindest in gewisser Weise als unterschiedliche parametrische Kurven betrachten. Dies mag wie ein Unterschied erscheinen, über den wir uns keine Sorgen machen müssen, aber wie wir in späteren Abschnitten sehen werden, kann dies ein sehr wichtiger Unterschied sein. In einigen der späteren Abschnitte benötigen wir eine Kurve, die genau einmal verfolgt wird.,
Bevor wir zu anderen Problemen übergehen, lassen Sie uns kurz anerkennen, was passiert, indem Sie \(t\) in eine nt in diesen Arten von parametrischen Gleichungen ändern. Wenn es sich um parametrische Gleichungen handelt, die nur Sinus und Kosinus betreffen, und beide dasselbe Argument haben, wenn wir das Argument von \(t\) in nt ändern, ändern wir einfach die Geschwindigkeit, mit der die Kurve verfolgt wird. Wenn \(n > 1\), erhöhen wir die Geschwindigkeit und wenn \(n < 1\), verringern wir die Geschwindigkeit.
Schauen wir uns noch ein paar Beispiele an.,
Bis zu diesem Punkt haben wir Beispiele gesehen, die den vollständigen Graphen, den wir durch Eliminieren des Parameters erhalten haben, verfolgen würden, wenn wir einen ausreichend großen Bereich von \(t\)’s. Im vorherigen Beispiel haben wir jedoch jetzt gesehen, dass dies nicht immer der Fall sein wird. Es ist mehr als möglich, einen Satz parametrischer Gleichungen zu haben, die kontinuierlich nur einen Teil der Kurve verfolgen. Wir können normalerweise feststellen, ob dies geschieht, indem wir nach Grenzen für \(x\) und \(y\) suchen, die uns durch die parametrische Gleichung auferlegt werden.,
Wir verwenden häufig parametrische Gleichungen, um den Pfad eines Objekts oder Partikels zu beschreiben. Schauen wir uns ein Beispiel dafür an.
Wir sollten an dieser Stelle eine kleine Warnung geben. Aufgrund der damit verbundenen Ideen konzentrierten wir uns auf parametrische Kurven, die Teile der Kurve mehr als einmal zurückverfolgten. Lassen Sie sich jedoch nicht zu sehr in die Idee verwickeln, dass dies immer passieren wird. Viele, wenn nicht die meisten parametrischen Kurven werden nur einmal verfolgt. Das erste, das wir uns angesehen haben, ist ein gutes Beispiel dafür. Diese parametrische Kurve wird niemals einen Teil von sich wiederholen.,
In diesem Abschnitt muss ein letztes Thema besprochen werden, bevor es weitergeht. Bisher haben wir mit parametrischen Gleichungen begonnen und den Parameter eliminiert, um die parametrische Kurve zu bestimmen.
Es gibt jedoch Zeiten, in denen wir in die andere Richtung gehen wollen. Bei einer Funktion oder Gleichung möchten wir möglicherweise einen Satz parametrischer Gleichungen dafür aufschreiben. In diesen Fällen sagen wir, dass wir die Funktion parametrisieren.
Wenn wir die Beispiele 4 und 5 als Beispiele nehmen, können wir dies für Ellipsen (und damit für Kreise) tun., In Anbetracht der Ellipse
\
wäre ein Satz parametrischer Gleichungen dafür
\
Dieser Satz parametrischer Gleichungen verfolgt die Ellipse beginnend am Punkt \(\left ({a,0} \right)\) und verfolgt sie gegen den Uhrzeigersinn und verfolgt sie genau einmal im Bereich \(0 \le t \le 2\pi \). Dies ist ein ziemlich wichtiger Satz parametrischer Gleichungen, der in einigen Fächern mit dem Umgang mit Ellipsen und/oder Kreisen kontinuierlich verwendet wird.
Jede Kurve kann auf mehr als eine Weise parametriert werden. Jedes der folgenden Parameter parametriert auch dieselbe Ellipse.,
\
Das Vorhandensein des \(\omega \) ändert die Geschwindigkeit, mit der sich die Ellipse dreht, wie wir in Beispiel 5 gesehen haben. Beachten Sie auch, dass die letzten beiden Ellipsen mit einer Bewegungsrichtung im Uhrzeigersinn verfolgen (dies möchten Sie möglicherweise überprüfen). Beachten Sie auch, dass nicht alle an derselben Stelle beginnen (wenn wir an \(t = 0\) als Ausgangspunkt denken).
Es gibt natürlich noch viele weitere Parametrierungen einer Ellipse, aber Sie bekommen die Idee. Es ist wichtig zu bedenken, dass jede Parametrierung die Kurve einmal mit einem potenziell anderen Bereich von \(t\)’s., Jede Parametrierung kann sich mit unterschiedlichen Bewegungsrichtungen drehen und an verschiedenen Punkten beginnen.
Möglicherweise benötigen Sie eine Parametrierung einer Ellipse, die an einer bestimmten Stelle beginnt und eine bestimmte Bewegungsrichtung hat, und so wissen Sie jetzt, dass Sie mit einiger Arbeit eine Reihe parametrischer Gleichungen aufschreiben können, die Ihnen das gewünschte Verhalten geben.
Lassen Sie uns nun einige andere wichtige Parametrierungen aufschreiben und alle Kommentare zu Bewegungsrichtung, Startpunkt und Bereich von \(t\) für eine Spur (falls zutreffend) sind immer noch wahr.,
Da ein Kreis nichts anderes als ein Sonderfall einer Ellipse ist, können wir die Parametrierung einer Ellipse verwenden, um auch die parametrischen Gleichungen für einen Kreis zu erhalten, der am Ursprung des Radius \(r\) zentriert ist. Eine Möglichkeit, einen Kreis zu parametrieren, besteht darin,
\ \
Zu diesem Zeitpunkt scheint es möglicherweise nicht so nützlich zu sein, eine solche Funktion zu parametrieren, aber es gibt viele Fälle, in denen es tatsächlich einfacher oder sogar erforderlich ist, mit der Parametrierung anstelle der Funktion selbst zu arbeiten., Leider treten fast alle diese Fälle in einem Calculus III-Kurs auf.
















Schreibe einen Kommentar