
Heute nehmen wir eine schauen Sie sich die beliebtesten Optionen Preismodell. Das Black-Scholes-Modell, auch als Black-Scholes-Merton-Methode bekannt, ist ein mathematisches Modell für die Preisgestaltung von Optionsverträgen. Es funktioniert, indem die Variation der Finanzinstrumente geschätzt wird. Die Technik beruht auf der Annahme, dass die Preise einer lognormalen Verteilung folgen. Basierend darauf leitet es den Wert einer Option ab.,
Es eignet sich eher für pfadunabhängige Optionen, die die Anleger vor Fälligkeit nicht ausüben können. Dies unterscheidet es vom binomialen Optionspreismodell, bei dem es sich um eine risikoneutrale Methode zur Bewertung von pfadabhängigen Optionen (z. B. amerikanische Optionen) handelt.
Analysten und Investoren betrachten Black Scholes als eines der wesentlichen Konzepte der modernen Finanztheorie.
Das 1973 im Journal of Political Economy von Fischer Black und Myron Scholes eingeführte und später von Robert Merton aufgebaute Modell gewann 1997 den Nobelpreis für Wirtschaft.,
Das Modell folgt einer Differentialgleichung, die wir für die Preise der Optionen lösen. Wir verwenden die Standardvariation des Modells für europäische Stiloptionen. Black Scholes eignet sich nicht für Optionen im amerikanischen Stil, da Anleger diese Optionen zu keinem Zeitpunkt vor ihrem Ablaufdatum ausüben können.
Die Methode geht davon aus, dass der Kurs der zugrunde liegenden Aktie einer lognormalen Verteilung folgt, da er nicht negativ sein kann. Die Verteilung, auf die sich das Modell stützt, basiert auf der Brownschen Bewegung, einer Theorie zur Vorhersage natürlich vorkommender zufälliger Phänomene.,
Wir verwenden das Modell, um eine Schätzung für den Preis einer Option anhand der folgenden Informationen zu berechnen:
- Der aktuelle Preis;
- Der Ausübungspreis;
- Zeit bis zum Ablauf;
- Erwartete Dividendenrendite;
- Erwarteter Zinssatz; und
- Erwartete Volatilität.
Zunächst berücksichtigt das Modell nicht die Auswirkungen von Dividendenauszahlungen. Daher wird dies häufig angepasst, indem der Ex-Dividenden-Datumswert des Basiswerts bestimmt wird., Die Dividendenrendite reduziert den aktuellen Aktienkurs, weil der Optionsinhaber auf die Dividenden verzichtet.
Annahmen
Das Black Scholes-Modell funktioniert nur, wenn wir bestimmte Annahmen treffen.,s während der Optionslebensdauer auftreten (dies war eine Annahme im ursprünglichen Modell, die Analysten seitdem durch Hinzufügen der Dividendenrendite in der Modellformel eliminiert haben);
Black Scholes Formula
Die Modellformel ist mathematisch recht komplex, was kein besonderes Problem darstellt, da wir sie mit speziellen Tools für uns berechnen können. Aber es ist immer noch wichtig zu verstehen, wie es funktioniert.,
Um den Preis einer Call-Option zu berechnen, können wir unter dem Black Scholes-Modell die folgende Gleichung verwenden:
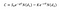
Wobei:
- S0 der Aktienkurs ist;
- e ist die Exponentialzahl;
- q ist der Prozentsatz der Dividendenrendite;
- T ist der Begriff (ein Jahr ist T=1, während sechs Monate T=0 sind.,5);
- N (d1) ist das Delta der Call-Option, dh die Änderung des Call-Preises gegenüber der Verschiebung des Aktienkurses;
- K ist der Ausübungspreis;
- r ist der risikofreie Kurs; und
- N(d2) ist die Wahrscheinlichkeit, dass der zukünftige Aktienkurs höher ist als der Ausübungspreis, die Wahrscheinlichkeit, dass wir die Option ausüben werden.
Eine Seite ist der Aktienkurs multipliziert mit der kumulativen Standardnormalverteilung von d1 und die andere — der Ausübungspreis, abgezinst auf Zeit T und dann multipliziert mit der kumulativen Standardnormalverteilung von d2.,
Wobei wir d1 und d2 mit folgenden Formeln berechnen können:
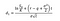
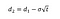
Wobei σ die Volatilität der Renditen des Basiswerts ist.,
Wir können die gleiche Logik für eine put-Option anwenden:

Besuchen Sie unseren Newsletter für eine KOSTENLOSE Excel Benchmark Analyse Vorlage
Beispiel Black Scholes Berechnung
Um das Konzept hinter dem Black Scholes Modell besser zu veranschaulichen, werfen wir einen Blick auf das folgende Modell. Wir beginnen mit den Modelleingaben., Wie oben diskutiert, benötigen wir die folgenden sechs Variablen, um den Aufruf zu berechnen und Optionswerte zu setzen.

Als nächstes berechnen wir die Parameter der Optionen. Beginnend mit d1 erhalten wir 0,39 aus unseren Modellannahmen.

Zu berechnen, wir übertragen einfach die Formel für d1 zu Excel.,
Following the same approach, we calculate d2, N(d1) and N(d2).

With those, we can calculate the Call Option Price and the Put Option Price.,

Wir beschäftigen kann den Anruf-Put-Parität-Regel, um zu überprüfen, ob unsere Formeln und Berechnungen korrekt sind.

Nachdem wir nun unser Modell haben, um die Preise für Aufrufe und Optionen zu berechnen, können wir einen Schritt weiter gehen und nach wie sich die verschiedenen Eingabeparameter auf die Ergebnisse unseres Modells auswirken., Die Datentabellenfunktionalität in Excel ist ein großartiges Werkzeug, um einige Sensitivitätsanalysetabellen für unsere Variablen vorzubereiten. In unserem Artikel zur Sensitivitätsanalyse erfahren Sie, wie Sie Datentabellen verwenden.
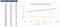
Schauen wir uns den Aktienkurs an, wenn er sich von 10 €auf 100 €ändert und wie er sich auf die Call-und Put-Werte auswirkt. Wir stellen fest, dass die Call-Option keinen Wert hat, bis der Aktienkurs 40 €erreicht. Wir sehen das Gegenteil für die Put-Option, bei der ihr Wert Null erreicht, sobald der Aktienkurs über 85 €liegt.,

Wenn wir dieselbe Empfindlichkeitstabelle für den Ausübungspreis vorbereiten, können wir den umgekehrten Trend beobachten.beziehung. Wenn der Ausübungspreis steigt, sinkt der Call-Wert und der Put-Wert steigt.

Schauen wir uns auch den risikofreien Kurs an., Wenn es zunimmt, erhöht dies auch die erforderliche Rendite. Anschließend verringert dies den Wert der Bestände. Wir bemerken eine direkte Beziehung, wenn der risikofreie Kurs steigt, steigt auch der Call-Option-Wert, während der Put-Option-Wert seinen Wert verringert.
Nach dem gleichen Ansatz können Sie sich den Rest der Seite ansehen.parameter und wie sie die Optionswerte beeinflussen., Sie können das Excel-Modell am Ende des Artikels herunterladen und dort die Empfindlichkeitsanalyse durchgehen.
Sie können das Beispielmodell in Excel im Originalartikel herunterladen.
Schlussfolgerung
Es ist wichtig zu bedenken, dass das Black-Scholes-Merton-Modell ein theoretisches Konzept ist. Wir verwenden es, um das Verhalten des Marktes abzuschätzen. Wenn wir jedoch die Ergebnisse in unserem Entscheidungsprozess verwenden, müssen wir die zugrunde liegenden Annahmen im Modell verstehen und wie es von der Realität abweicht.,
Die Formel half dem Optionshandel, populärer zu werden, da es weniger nach Glücksspiel aussieht. Heutzutage sind verschiedene Modifikationen von Black Scholes als grundlegende Strategien zur Risikokontrolle, die mit Volatilität verbunden sind, weit verbreitet.
Sie können Ihre Unterstützung zeigen, indem Sie den Artikel mit Kollegen und Freunden teilen.
















Schreibe einen Kommentar