Ein Vektor hat Größe (wie lang er ist) und Richtung:
Hier sind zwei Vektoren:

Sie können mit dem „Punktprodukt“ multipliziert werden (siehe auch Kreuzprodukt).,
Wir können das Punktprodukt zweier Vektoren auf diese Weise berechnen:

a · b = |a| × |b| × cos(θ)
Wobei:
|a| ist die Größe (Länge) des Vektors a
|b| ist die Größe (Länge) des Vektors b
θ ist der Winkel zwischen a und b
Also multiplizieren wir die Länge von a mit der Länge von b, multiplizieren Sie dann mit dem Kosinus des Winkels zwischen a und b
ODER wir können es auf diese Weise berechnen:
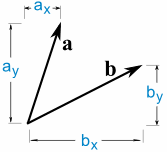
a · b = ax × bx + ay × by
Also multiplizieren wir die x ’s, multiplizieren y‘ s, dann hinzufügen.,
Beide Methoden funktionieren!
Und das Ergebnis ist eine Zahl („Skalar“ genannt, damit wir wissen, dass es kein Vektor ist).
Hinweis:Sie können den Vektor Calculatorto Ihnen helfen.
Warum cos(θ) ?
OK, um zwei Vektoren zu multiplizieren, ist es sinnvoll, ihre Längen miteinander zu multiplizieren, aber nur, wenn sie in die gleiche Richtung zeigen.,
Also machen wir einen „Punkt in die gleiche Richtung“ wie den anderen, indem wir mit cos(θ) multiplizieren:
 |
 |
|
| Wir nehmen die Komponente eines , die neben b liegt |
Wie ein Licht scheint, um zu sehen wo der Schatten liegt |
DANN wir multiplizieren !,
Rechtwinklig
Wenn zwei Vektoren rechtwinklig zueinander stehen, ist das Punktprodukt Null.
Dies kann eine praktische Möglichkeit sein, um herauszufinden, ob zwei Vektoren im rechten Winkel sind.
Drei oder mehr Dimensionen
Das alles funktioniert auch in 3 (oder mehr) Dimensionen.
Und kann tatsächlich sehr nützlich sein!
Ich habe einmal eine solche Berechnung ausprobiert, aber alles in Winkeln und Entfernungen gearbeitet … es war sehr schwer, beteiligt viele Trigonometrie, und mein Gehirn verletzt. Die obige Methode ist viel einfacher.,
Kreuzprodukt
Das Punktprodukt gibt eine skalare Antwort (gewöhnliche Zahl) und wird manchmal als Skalarprodukt bezeichnet.
Aber es gibt auch das Kreuzprodukt, das einen Vektor als Antwort gibt und manchmal als Vektorprodukt bezeichnet wird.

















Schreibe einen Kommentar