Gehen Sie zu Oberfläche oder Volumen.
Ein Prisma ist ein festes Objekt mit:
- identischen Enden
- flachen Flächen
- und dem gleichen Querschnitt entlang seiner gesamten Länge !
Ein Querschnitt ist die Form, die durch Schneiden direkt über ein Objekt hergestellt wird.
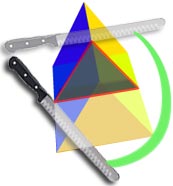
Der Querschnitt dieses Objekt ist ein Dreieck …
.. es hat den gleichen Querschnitt entlang seiner gesamten Länge …
… es ist also ein dreieckiges Prisma.,
|
Versuchen Sie, eine Form auf ein Stück Dann stellen Sie sich vor, es erstreckt sich vom Blatt Papier… |
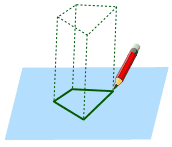 |
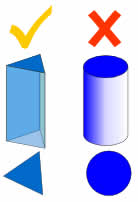
Keine Kurven!
Ein Prisma ist ein Polyeder, was bedeutet, dass alle Flächen flach sind!
Keine gekrümmten Seiten.
Zum Beispiel ist ein Zylinder kein Prisma, weil er gekrümmte Seiten hat.,
Basen
Die Enden eines Prismas sind parallel
und jeder wird als Basis bezeichnet.
Seiten
Die Seitenflächen eines Prismas sind Parallelogramme
(4-seitige Formen mit gegenüberliegenden Seiten parallel)
Das sind alles Prismen:
und mehr!

Beispiel: Dieser sechseckige Eiskristall.
Es sieht aus wie ein Sechseck, aber weil es hat eine gewisse Dicke, ist es eigentlich ein sechseckiges PRISMA!
Foto von NASA / Alexey Kljatov.,
Reguläre vs unregelmäßige Prismen
Alle vorherigen Beispiele sind reguläre Prismen, da der Querschnitt regelmäßig ist (mit anderen Worten, es ist eine Form mit gleichen Kantenlängen und gleichen Winkeln.,)
Here is an example of an Irregular Prism:
| Irregular Pentagonal Prism: | ||
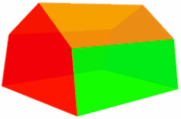 |
 |
|
| Cross-Section | ||
| It is „irregular“ because the cross-section is not „regular“ in shape.,div> Oberfläche = 2 × Basis Bereich
+ Basis Umfang × Länge Beispiel: Was ist die oberfläche von ein prisma wo die basis bereich ist 25 m2, die basis umfang ist 24 m, und die länge ist 12 m: Oberfläche = 2 × Basis Bereich + Basis Umfang × Länge
= 2 × 25 m2 + 24 m × 12 m
= 50 m2 + 288 m2
= 338 m2
(Hinweis: Wir haben ein Flächenberechnungswerkzeug) Volumen eines PrismasDas Volumen eines Prismas ist die Fläche eines Endes mal die Länge des Prismas., Volume = Base Area × Length Beispiel: Wie groß ist das Volumen eines Prismas, bei dem die Grundfläche 25 m2 beträgt und das 12 m lang ist: Volume = Area × Length
= 25 m2 × 12 m
= 300 m3
Spielen Sie hier damit., Die Formel funktioniert auch, wenn sie sich „beugt“ (schräg), aber denken Sie daran, dass die Höhe im rechten Winkel zur Basis steht: Und deshalb:
© 2021 Tombouctou Theme von Anders Norén — Hoch ↑ | ||






















Schreibe einen Kommentar