Mobiler Hinweis anzeigen Alle Notizen anzeigen Ausblenden Aller Notizen
Abschnitt 4-7: Lineare Annäherungen
In diesem Abschnitt werden wir uns eine Anwendung nicht von Derivaten, sondern von der Tangente zu einer Funktion ansehen. Um die Tangente zu bekommen, müssen wir natürlich Derivate nehmen, also ist dies in gewisser Weise auch eine Anwendung von Derivaten.
\
Schauen Sie sich das folgende Diagramm einer Funktion und ihrer Tangente an.
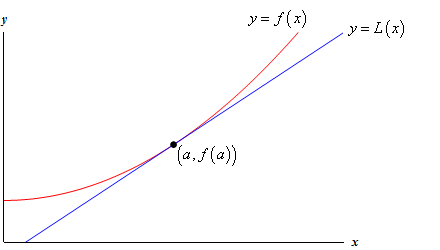
Also, warum sollten wir das tun? Schauen wir uns ein Beispiel an.,
Lineare Approximationen nähern sich Werten von \(f\left( x \right)\) sehr gut an, solange wir „in der Nähe“ \(x = a\) bleiben. Je weiter wir jedoch von \(x = a\) entfernt sind, desto schlechter wird die Approximation. Das Hauptproblem hierbei ist, dass die Nähe zu \(x = a\), um eine gute Annäherung zu erhalten, sowohl von der von uns verwendeten Funktion als auch von dem von uns verwendeten Wert von \(x = a\) abhängt. Außerdem wird es oft keine einfache Möglichkeit geben vorherzusagen, wie weit wir von \(x = a\) entfernt sind und immer noch eine „gute“ Annäherung haben.,
Schauen wir uns ein anderes Beispiel an, das an einigen Stellen tatsächlich ziemlich stark verwendet wird.
Dies ist eigentlich eine etwas wichtige lineare Annäherung. In der Optik wird diese lineare Annäherung häufig verwendet, um Formeln zu vereinfachen. Diese lineare Annäherung wird auch verwendet, um die Bewegung eines Pendels und Schwingungen in einer Saite zu beschreiben.
















Schreibe einen Kommentar