Dreieck-Abbildung Winkel-Seite-Winkel (ASA)
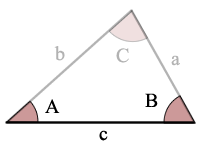
A = Winkel A
B = Winkel B
C = Winkel C
a = Seite a
b = b-Seite
c = Seite c
P = perimeter
s = semi-perimeter
K = Bereich
r = radius des inkreises
R = radius des umschriebenen Kreises
Rechner Verwenden
Jede Berechnung option, wie unten gezeigt, hat sub-Aufzählungszeichen, die Liste die Reihenfolge der Methoden in diesem Rechner zu lösen für unbekannte Winkel und Seite-Werte einschließlich der Summe der Winkel in einem Dreieck, das Gesetz von Sines und Gesetz des Cosinus., Dies sind NICHT die EINZIGEN Sequenzen, mit denen Sie diese Art von Problemen lösen können.
- Siehe auch diese Trigonometrie Taschenrechner:
- Gesetz der Kosinus Rechner
- Gesetz der Sinus Rechner
Lösen Dreieck Theoreme
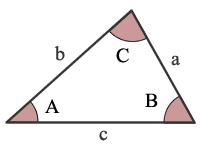
AAA ist Winkel, Winkel, Winkel
Angabe der drei winkel eines dreiecks nicht identifizieren Sie ein Dreieck eindeutig. Wenn Sie daher zwei Winkel eines Trigles angeben, können Sie nur den dritten Winkel berechnen.,
Angesichts der Größe von 2 Winkeln eines Dreiecks können Sie die Größe des dritten Winkels berechnen. Die Summe entspricht 180° oder π Bogenmaß.
C = 180° – A-B (in Grad)
C = π – A – B (im Bogenmaß)
AAS ist Winkel, Winkel, Seite
Bei der Größe von 2 Winkeln und 1 Seite gegenüber einem der angegebenen Winkel können Sie die Größe des verbleibenden 1 Winkels und 2 Seiten berechnen.
Verwenden Sie die Regel Summe der Winkel, um den anderen Winkel zu finden, dann
Verwenden Sie das Sinusgesetz, um für jede der beiden anderen Seiten zu lösen.,
ASA ist Winkel, Seite, Winkel
Angesichts der Größe von 2 Winkeln und der Größe der Seite, die sich zwischen diesen 2 Winkeln befindet, können Sie die Größe des verbleibenden 1 Winkels berechnen und 2 Seiten.
Verwenden Sie die Regel Summe der Winkel, um den anderen Winkel zu finden, dann
Verwenden Sie das Sinusgesetz, um für jede der beiden anderen Seiten zu lösen.,
ASS (oder SSA) ist Winkel, Seite, Seite
Angesichts der Größe von 2 Seiten (a und c, wobei a < c) und der Größe des Winkels A, der sich nicht zwischen diesen beiden Seiten befindet, können Sie möglicherweise die Größe der verbleibenden 1 Seite und 2 Winkel berechnen, abhängig von den folgenden Bedingungen.,f-Kosinus zum Lösen für jeden der beiden anderen Winkel
Präsentieren Sie 2 vollständige Lösungen
Beispiel: 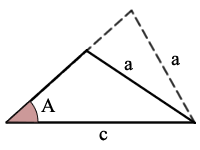
sin(A) = a/c, es gibt ein mögliches Dreieck
Verwenden Sie das Sinusgesetz, um für einen Winkel zu lösen, C
Verwenden Sie die Summe der Winkelregel, um den anderen Winkel zu finden, B
erwenden Sie das Gesetz der Sinus für die letzte Seite zu lösen, b
Beispiel: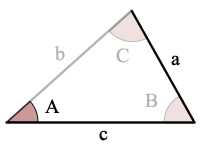
sin(A)> a/c, gibt es keine möglichen dreiecke
Fehler Hinweis: sin(A)> a/c so gibt es keine Lösungen und kein Dreieck!,
Beispiel: 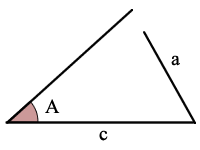
SAS ist Seite, Winkel, Seite
Angesichts der Größe von 2 Seiten (c und a) und der Größe des Winkels B, der zwischen diesen beiden Seiten liegt, können Sie die Größe der verbleibenden 1 Seite und 2 Winkel berechnen.
Verwenden Sie das Kosinusgesetz, um für die verbleibende Seite zu lösen, b
Bestimmen Sie, welche Seite, a oder c, am kleinsten ist, und verwenden Sie das Sinusgesetz, um für die Größe des entgegengesetzten Winkels A oder C zu lösen.,
Verwenden Sie die Regel Summe der Winkel, um den letzten Winkel zu ermitteln
SSS ist Seite, Seite, Seite
Angesichts der Größen der 3 Seiten können Sie die Größen aller 3 Winkel im Dreieck berechnen.
Verwenden Sie das Gesetz der Kosinus für die Winkel zu lösen. Sie können auch die Regel Summe der Winkel verwenden, um den endgültigen Winkel zu ermitteln, sobald Sie 2 davon kennen.,sin-1
Kosinusgesetz
Wenn a, b und c die Längen der Schenkel eines Dreiecks gegenüber den Winkeln A, B und C sind; dann besagt das Gesetz der Kosinus:
a2 = c2 + b2 – 2bc cos A, Lösen für cos A, cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, Lösen für cos B, cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos, Lösen für cos C, cos C = ( a2 + b2 – c2 ) / 2ab
Lösen, zum Beispiel für einen Winkel, A = cos-1
Andere Dreieckseigenschaften
Dreiecksumfang, P = a + b + c
Dreieckshalbumfang, s = 0.,5 * (a + b + c)
Dreiecksfläche, K = √
Radius des eingeschriebenen Kreises im Dreieck, r = √
Radius des umschriebenen Kreises um das Dreieck, R = (abc) / (4K)
Referenzen/ Weiterlesen
Weisstein, Eric W. „ASS Theorem.“Von MathWorld – Eine Wolfram Web-Ressource. ASS-Satz.
Mathe macht Spaß beim Lösen von SAS-Dreiecken
















Schreibe einen Kommentar