Ganzzahl, Absoluter Wert: Einfache Definition und Beispiele, Programmierung

Statistiken Definitionen >

Inhalt:

• Definition
• Absoluter Wert
• Ganzzahlige Programmierung

Definition

Der Satz von ganzen Zahlen erhält häufig das Symbol Z und Z ist definiert als

{…, -3, -2,-1, 0, 1, 2, 3,…}

Es gibt eine unendliche Anzahl von ganzen Zahlen., Sie können bestellt werden, indem sie auf einer Zahlenzeile platziert werden; Die Zahl nach rechts ist immer größer als die nach links.

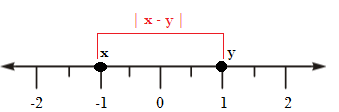
Eine Reihe Zeile zeigt die Entfernung zwischen -1 und 1.

Absoluter Wert einer Ganzzahl

Der absolute Wert einer Ganzzahl ist der Abstand von dieser Zahl zum Ursprung (0). Da sowohl 3 als auch -3 3 Einheiten (Schritte) vom Ursprung entfernt sind, ist der absolute Wert beider Zahlen 3.,

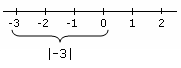
Der absolute Wert von -3 ist 3, da es drei Räume, von null auf der Zahlengeraden.

Vorzeichen

Addition und Subtraktionen

Um zwei Ganzzahlen mit unterschiedlichen Vorzeichen hinzuzufügen, ermitteln Sie die Differenz der Absolutwerte und geben Sie die Differenz an dasselbe Vorzeichen wie die Zahl mit dem größten Absolutwert.
Beispiel: (-5) + (3)

1. Finden Sie die absoluten Werte (5 und 3).
2. Finde den Unterschied zwischen 5 und 3 (5 – 3 = 2).
3. Finden Sie das Vorzeichen des größten absoluten Wertes. -5 hat ein negatives Vorzeichen.,
4. Fügen Sie das Zeichen von Schritt 3 zu dem Unterschied hinzu, den Sie in Schritt 2 gefunden haben. Das Ergebnis ist -2.

Wenn eine Ganzzahl zu einer anderen addiert oder subtrahiert wird, ist das Ergebnis immer eine Ganzzahl.

Multiplikation

Um eine ganze Zahl zu multiplizieren, multiplizieren Sie den absoluten Wert. Wenn die beiden multiplizierten Ganzzahlen dasselbe Vorzeichen haben, ist das Ergebnis positiv. Wenn die beiden ganzen Zahlen unterschiedliche Vorzeichen haben, ist das Ergebnis negativ.

Wenn eine Ganzzahl mit einer anderen multipliziert wird, ist das Ergebnis immer eine Ganzzahl. Aber wenn man durch einen anderen geteilt wird, kann das Ergebnis eine ganze Zahl sein oder auch nicht., Zum Beispiel, während 3/3 = 1 und 8/4 = 2 und ganze Zahlen sind, 3/4 und 8/5 nicht.

Integer-Programmierung

Integer-Programmierung (IP) Probleme sind eine Art von Machbarkeits-oder mathematischen Optimierungsproblem, bei dem einige (oder alle) der Variablen auf ganzzahlige Werte beschränkt sind.

• Wenn alle Variablen auf Ganzzahlen beschränkt sind, wird das IP-Problem als IP-Problem (Pure Integer Programming) bezeichnet.
• Wenn Variablen eine Mischung zwischen erforderlichen Ganzzahlen und anderen ohne solche Einschränkung sind, wird das IP-Problem als gemischtes IP-Problem bezeichnet.,
• Wenn die Ganzzahlen auf 0 oder 1 beschränkt sind, wird das Problem als rein-oder gemischt bezeichnet&mdas;binary integer programming problem.

Manchmal wird der Begriff IP verwendet, um sich auf ganzzahlige lineare Programmierung zu beziehen, eine Art der Programmierung, bei der sowohl die Zielfunktion als auch alle nicht ganzzahligen Einschränkungen linear sind.

Modellierung mit IP-Problemen

Wann werden IP-Probleme verwendet? Oft um reale Probleme zu modellieren, bei denen Werte natürlich auf ganze Zahlen beschränkt sind., Wenn wir beispielsweise die Computerproduktion in einer Fabrik in China mit einfachen linearen Programmiermodellen modellieren, könnten wir einen Plan mit 2067, 4 Computern pro Monat erstellen. Dass „.4 “ macht keinen intuitiven Sinn; Wie kann eine Fabrik 40% eines Computers produzieren (obwohl ich annehme, dass sie die Linie anhalten könnten, wenn das .4 eines Computers ist fertig!). Wir könnten es runden, würden es aber vorziehen, wenn es überhaupt eine ganze Zahl wäre.

Manchmal machen nicht ganzzahlige Variablen noch weniger Sinn. Beispielsweise kann ein lineares Programmiermodell, dem Lehrer bestimmten Städten zugewiesen werden, empfehlen, 0 zu platzieren.,7 lehrer in einer Stadt und 0,5 in einer anderen. Wir brauchen eine Möglichkeit, Modelle zu erstellen, die die ganzen Zahlen einiger oder aller Variablen berücksichtigen.

Das Formulieren und Lösen von IP-Problemen

Das Formulieren von IPs ist typischerweise schwieriger als das Formulieren einfacher linearer Programme. Obwohl es einige Tricks gibt, ist der Schlüssel Übung.

Es gibt keine allgemeinen, recheneffektiven Algorithmen zum Lösen von IPs analog zu denen, die für lineare Programme verwendet werden., Stattdessen müssen Sie normalerweise zwischen allgemeinen, rechnerisch ineffektiven Lösungsmethoden wählen oder einen Spezialalgorithmus entwerfen, der genau dieses spezifische Problem angreifen kann.

——————————————————————————

Benötigen Sie Hilfe bei Hausaufgaben oder Testfragen?, Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor ist kostenlos!