Männer. Ich fühle irgendwie, dass ich mag, was du sagst.
Soc. Und ich, Meno, mag, was ich sage.
aus Platons Meno
Die Länge der Diagonale des Einheitsquadrats entspricht der Quadratwurzel von 2.
Die Länge der Diagonale des Einheitsquadrats entspricht √2. Nun, das sind keine wirklich guten Nachrichten. Jeder, der jemals auf den Satz des Pythagoras gestoßen ist, ist sich der Tatsache bewusst., Im gleichschenkligen rechtwinkligen Dreieck mit den Beinen der Länge 1 hat die Hypotenuse nach dem Satz von Pythagoras – 12 + 12 = (Hypotenuse)2 – tatsächlich die Länge √2. Die Motivation für diese Seite ist nicht so sehr diese Tatsache selbst, sondern die Art, sie ohne Rückgriff auf den berühmten Satz zu zeigen. In der Tat könnte argumentiert werden, dass der Satz des Pythagoras überstrapaziert worden sein könnte, siehe ein merkwürdiges Beispiel.
Ein Argument, das auf die Figur von Sokrates in Platons Meno zurückgeht, könnte Pythagoras selbst bekannt gewesen sein, obwohl dieser ein Jahrhundert zuvor lebte.,
Im Dialog führt Sokrates auf seine übliche Weise einen jungen Sklaven zu einer Konstruktion eines Quadrats, das doppelt so groß ist wie die Fläche des gegebenen:
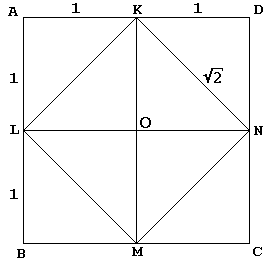
Das gegebene Quadrat KLMN mit Zentrum O wird zuerst durch seine Diagonalen in 4 gleiche Dreiecke geschnitten. Sokrates bettet KLMN in ein größeres Quadrat ABCD ein, als ob es diese Dreiecke jeweils in seiner Hypotenuse widerspiegeln würde. Der Sklave gibt dann zu – und wer nicht? – das Quadrat ABCD ist doppelt so groß wie Quadrat KLMN.
Um ehrlich zu sein, Sokrates‘ Quadrat ABCD gemessen 4 auf der Seite, so dass Platz KLMN hatte Fläche von 8., Es ist klar, dass, wenn wir mit dem Quadrat ABCD von Seite 2 (und damit von Bereich 4) beginnen, das Quadrat KLMN eine Fläche von 2 hat.
Nun ist √A im Allgemeinen für eine positive Zahl A definiert als eine Zahl, deren Quadrat A ist:
(√A)2.
Andererseits weiß jeder Flächenschüler, dass die Fläche eines Quadrats der Seite b gleich b2 ist. Daraus folgt, dass die Seite eines Quadrats mit der Fläche A genau √A.Wir schließen daraus, dass die Seite des Quadrats KLMN gleich √2. Zum einen
KN = √A.
Der zentrale Punkt des Arguments ist die Tatsache, dass KN im Diagramm eine doppelte Rolle spielt., Es ist nicht nur eine der Seiten des quadratischen KLMN, sondern dient auch als Diagonale des quadratischen OKDN. Letzteres ist natürlich ein Einheitsquadrat, was unsere Behauptung beweist.
(Aus einer etwas anderen Perspektive wird dieselbe Episode an anderer Stelle erwähnt.)
















Schreibe einen Kommentar