Wurzeln eines Polynoms

Eine Wurzel oder Null einer Funktion ist eine Zahl, die beim Einstecken für die Variable die Funktion gleich Null macht. Somit sind die Wurzeln eines Polynoms P(x) Werte von x, so dass P(x) = 0 ist.

Der rationale Nullensatz

Der rationale Nullensatz besagt:

Wir können den rationalen Nullensatz verwenden, um alle rationalen Nullen eines Polynoms zu finden., Hier sind die Schritte:

  1. Ordnen Sie das Polynom in absteigender Reihenfolge an
  2. Notieren Sie alle Faktoren des konstanten Terms. Dies sind alle möglichen Werte von p.
  3. Notieren Sie alle Faktoren des führenden Koeffizienten. Dies sind alle möglichen Werte von q.
  4. Notieren Sie alle möglichen Werte von . Denken Sie daran, dass, da Faktoren negativ sein können, und – beide enthalten sein müssen. Vereinfachen Sie jeden Wert und streichen Sie alle Duplikate aus.,
  5. Verwenden Sie die synthetische Division, um die Werte von zu bestimmen, für die P () = 0 ist. Diese sind alle rationalen Wurzeln von P(x).

Beispiel: Finden Sie alle rationalen Nullstellen von P(x) = x3 -9x + 9 + 2×4 -19×2.

Bild %: Synthetische Division

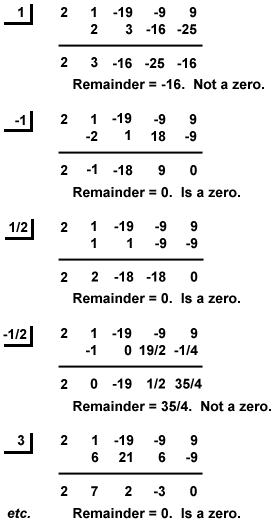
– Also der rationale Wurzeln von P(x) sind x = – 3, -1, 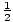und 3.

Wir können oft den rationalen Nullen-Satz verwenden, um ein Polynom zu faktorisieren., Mit synthetischer Division können wir eine reelle Wurzel a finden und den Quotienten finden, wenn P(x) durch x – a geteilt wird. Als nächstes können wir synthetische Division verwenden, um einen Faktor des Quotienten zu finden. Wir können diesen Prozess fortsetzen, bis das Polynom vollständig berücksichtigt wurde.