vektorer er i vid udstrækning nyttige i videnskaben til at beskrive noget, der har både en retning og en størrelse. De tegnes normalt ved hjælp af spidse pile, hvis længde repræsenterer vektorens størrelse. En passuarterbacks pass er det enkle eksempel, fordi det har retningen normalt et sted nede og en størrelse. Nogle gange er vi nødt til at håndtere to vektorer sammen, der arbejder på et objekt. I sådanne tilfælde er vinkler mellem disse vektorer vigtige., Dette emne vil forklare vinklen mellem to vektorer formel samt eksempler. Lad os lære det!
begrebet vektorer
uden for feltet kan vektorer bruges til at repræsentere et vilkårligt antal fysiske objekter eller aktiviteter. Eksempel. Vind er for eksempel en vektoriel mængde. Det skyldes, at det på ethvert givet sted har en retning såvel som størrelsen. Vi kan lave et kort over luftstrømmen på ethvert tidspunkt ved at tegne vindvektorer for en række forskellige geografiske placeringer.
mange egenskaber ved bevægelige objekter er også slags vektorer., I billardkugle beskriver dens hastighedsvektor dens bevægelse. Det viser retningen af vektorpilen mærker som bevægelsesretningen, og længden af vektoren repræsenterer kuglens hastighed.
billardkuglens momentum er også et eksempel på vektoriel mængde. Da det er lig med masse gange hastighed. Derfor er momentumvektoren af boldpunkterne i samme retning som dens hastighedsvektor. Og momentumvektorens størrelse vil være multiplikationsproduktet af boldens hastighed og dens masse.,
med hensyn til matematik er en vektor ethvert objekt, der har en definerbar størrelse og retning. Da vektorer ikke er de samme som standardlinjer eller figurer, skal vi bruge nogle specielle formler til at finde vinkler mellem dem.
Formlen for Vinklen mellem To Vektorer
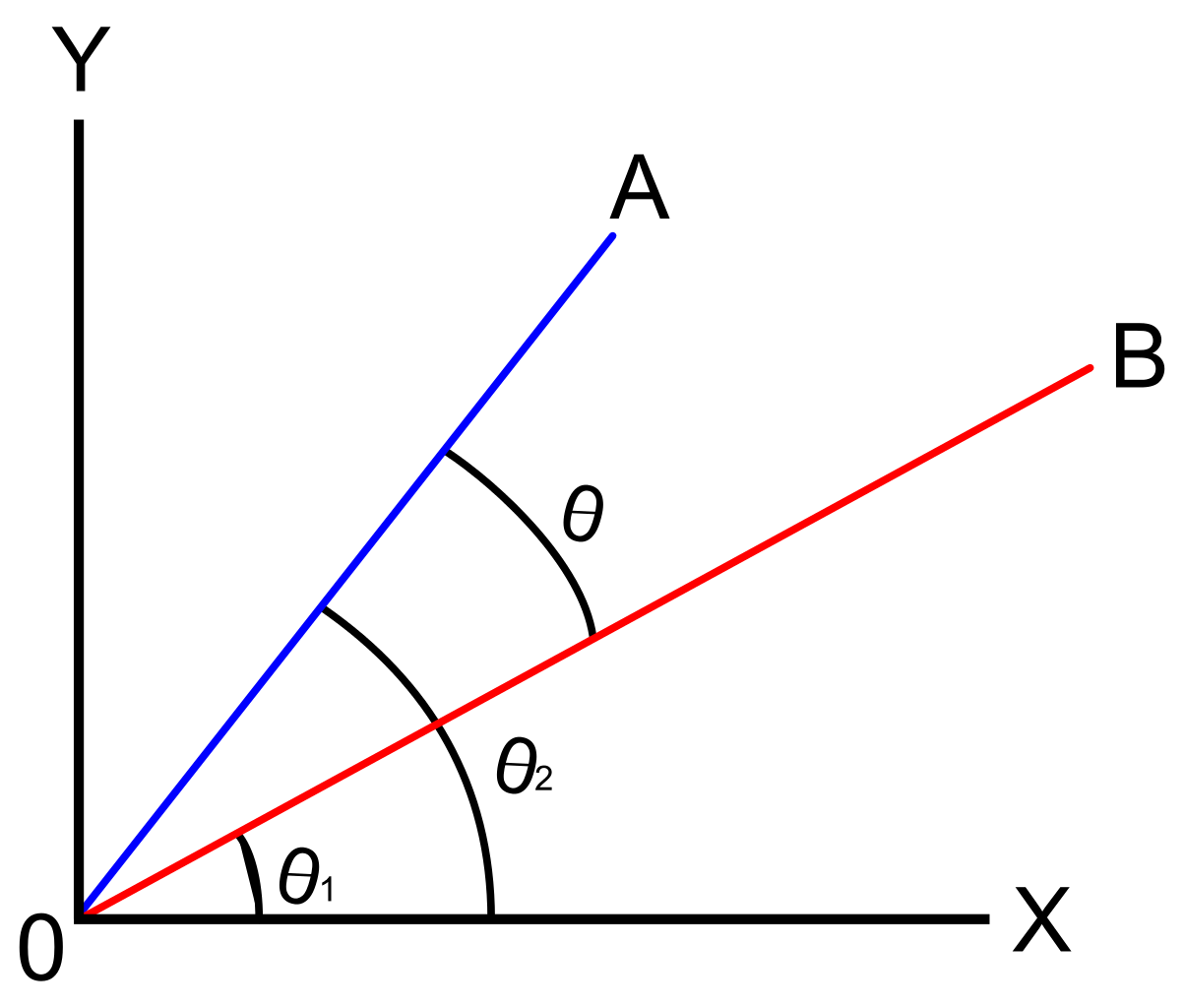
vinklen mellem to vektorer, vil blive udskudt i en enkelt pointe, som er kaldet som den korteste vinkel, hvor vi er nødt til at vende rundt en af de vektorer til placeringen af co-retningsbestemt med en anden vektor.,
diskussionen om retningsvinkler af vektorer fokuserer på at finde vinklen på en vektor i forhold til den positive.-akse. Dette vil fokusere på vinklen mellem to vektorer i standardpositionen. En vektor siges at være i standard position, hvis dens oprindelige punkt er oprindelsen (0, 0).
hvis de to vektorer antages som a og b, defineres den oprettede prik som a .b. Lad os antage, at disse to vektorer er adskilt af vinkel \(\theta\). At vide, hvad der er vinkelmålingen, vi vil løse ved hjælp af den givne formel:
Vi kender prikproduktet:
\(\vec{a}.,\vec{B} =|\vec{a}||\vec{B}|cos\theta\)
nu er vinklen mellem to vektorer formel:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{B}}{|\vec{a}||\vec{b}|}\)
hvor \\(theta\) er vinklen mellem A-og b-vektorer.
Løst Eksempler for Vinklen mellem To Vektorer Formel
Q. 1: Beregn vinklen mellem to vektorer, 3i + 4j – k og 2i – j + k.
Løsning: Lad,
en = 3i + 4j – k og
b = 2i – j + k
Vi definere dot produkt som:
en .b = (3i + 4j-k).(2i-j + k)
















Skriv et svar