Sandsynligheden for at rulle to terninger med seks-sidet dotssuch som 1, 2, 3, 4, 5 og 6 prikker i hver dør.

når to terninger kastes samtidigt, kan antallet af begivenheder således være 62 = 36, fordi hver terning har 1 til 6 tal på sine ansigter. Derefter vises de mulige resultater i nedenstående tabel.,
Sandsynlighed – Prøve plads til to terninger (resultater):
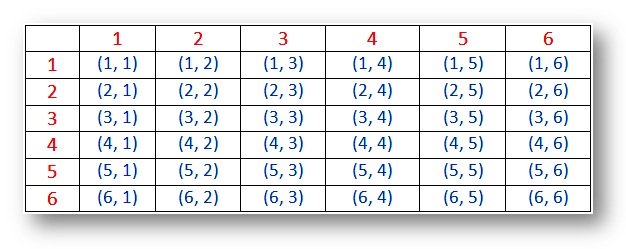
Bemærk:
(jeg) resultaterne (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) og (6, 6) kaldes dubletter.
(ii) parret (1, 2) og (2, 1) er forskellige resultater.
udarbejdede problemer med Sandsynlighed for rullende to terninger:
1. To terninger er rullet. Lad A, B, C være begivenhederne for at få en sum af 2, en sum af 3 og en sum af 4 henholdsvis., Derefter, viser, at
(i) Et er en enkel begivenhed
(ii) B og C er sammensat af begivenheder
(iii) A og B er gensidigt udelukkende
Løsning:
det er Klart, vi har
A = {(1, 1)}, B = {(1, 2), (2, 1)} og C = {(1, 3), (3, 1), (2, 2)}.
(i) Da A består af et enkelt prøvepunkt, er det en simpel begivenhed.
(ii) da både B og C indeholder mere end et prøvepunkt, er hver enkelt af dem en sammensat begivenhed.
(iii) da A ∩ B = ∅, A og B udelukker hinanden.
2. To terninger er rullet., A er den begivenhed, at summen af de tal, der vises på de to terninger er 5, og B er den begivenhed, at mindst en af terningerne viser en 3.
er de to begivenheder (i) gensidigt eksklusive, (ii) udtømmende? Giv argumenter til støtte for dit svar.
løsning:
Når to terninger rulles, har vi n (S) = (6 × 6) = 36.
Nu, En = {(1, 4), (2, 3), (4, 1), (3, 2)}, og
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(jeg) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
derfor udelukker A og B ikke hinanden.,
(ii) også A B B S. S.
derfor er A og B ikke udtømmende begivenheder.
flere eksempler relateret til spørgsmålene om sandsynlighederne for at kaste to terninger.
3. To terninger kastes samtidigt.,) at få en doublet
(v) at få en sum af 8
(vi) at få sum deles med 5
(vii) at få summen af atleast 11
(viii) at få et multiplum af 3 som summen
(ix) få en samlet atleast 10
(x) få en endnu antallet som summen
(xi) at få et primtal som en sum
(xii) at få en dublet af lige tal
(xiii) få et multiplum af 2 på en dør og et multiplum af 3 på den anden dør
Løsning:
To forskellige terningerne er kastet samtidig at være nummer 1, 2, 3, 4, 5 og 6 på deres ansigter., Vi ved, at i et enkelt kastet af to forskellige terninger er det samlede antal mulige resultater (6 6 6) = 36.
(i) at få seks som et produkt:
lad E1 = tilfælde af at få seks som et produkt. De tal, hvis produkt er seks vil være E1 = = 4
Derfor, sandsynlighed ofgetting ‘seks som et produkt”
Antallet af gunstige udfald
P(E1) = det Samlede antal mulige udfald
= 4/36
= 1/9
(ii) at få sum ≤ 3:
Lad E2 = begivenhed for at få summen ≤ 3., Det tal hvis sum ≤ 3 vil være E2 = = 3
Derfor, sandsynlighed ofgetting ‘sum ≤ 3″
Antallet af gunstige udfald
P(E2) = det Samlede antal mulige udfald
= 3/36
= 1/12
(iii) at få sum ≤ 10:
Lad E3 = begivenhed for at få summen ≤ 10. Det tal hvis sum ≤ 10 vil være E3 =
= 33
Derfor, sandsynlighed ofgetting ‘sum ≤ 10’
Antallet af gunstige udfald
P(E3) = det Samlede antal mulige udfald
= 33/36
= 11/12
(iv)at få en dublet:Lad E4 = begivenhed for at få en dublet., Det tal, som doublet vil være E4 = = 6
Derfor, sandsynlighed ofgetting ‘en doublet’
Antallet af gunstige udfald
P(E4) = det Samlede antal mulige udfald
= 6/36
= 1/6
(v)at få en sum af 8:
Lad E5 = tilfælde af at få en sum af 8. Det tal, som er en sum af 8 vil blive E5 = = 5
Derfor, sandsynlighed ofgetting ‘en sum af 8″
Antallet af gunstige udfald
P(E5) = det Samlede antal mulige udfald
= 5/36
(vi)at få sum deles med 5:
Lad E6 = begivenhed for at få sum deles med 5., Det tal hvis sum er delelig med 5, vil blive E6 = = 7
Derfor, sandsynlighed ofgetting ‘sum deles med 5″
Antallet af gunstige udfald
P(E6) = det Samlede antal mulige udfald
= 7/36
(vii)at få summen af atleast 11:
Lad E7 = begivenhed for at få summen af atleast 11. De begivenheder, der for summen af atleast 11 vil være E7 = = 3
Derfor, sandsynlighed ofgetting “summen af atleast 11′
Antallet af gunstige udfald
P(E7) = det Samlede antal mulige udfald
= 3/36
= 1/12
(viii) at få amultiple af 3 som summen:
Lad E8 = begivenhed for at få et multiplum af 3 som summen., De begivenheder, af et multiplum af 3 som summen vil blive E8 = = 12
Derfor, sandsynlighed ofgetting ‘et multiplum af 3 som summen”
Antallet af gunstige udfald
P(E8) = det Samlede antal mulige udfald
= 12/36
= 1/3
(ix) at få en totalof atleast 10:
Lad E9 = begivenhed for at få en total af atleast 10., De begivenheder, af i alt atleast 10 vil være E9 = = 6
Derfor, sandsynlighed ofgetting ‘alt atleast 10’
Antallet af gunstige udfald
P(E9) = det Samlede antal mulige udfald
= 6/36
= 1/6
(x) for at få en evennumber som summen:
Lad E10 = begivenhed for at få et lige antal som sum., Begivenheder for en selv antallet som summen vil blive E10 = = 18
Derfor, sandsynlighed ofgetting ‘en selv antallet som summen
Antallet af gunstige udfald
P(E10) = det Samlede antal mulige udfald
= 18/36
= 1/2
(xi) at få en primenumber som summen:
Lad E11 = begivenhed for at få et primtal som en sum., Begivenheder for et primtal som en sum vil være E11 = = 15
Derfor, sandsynlighed ofgetting ‘et primtal som en sum’
Antallet af gunstige udfald
P(E11) = det Samlede antal mulige udfald
= 15/36
= 5/12
(xii) at få adoublet af lige tal:
Lad E12 = begivenhed for at få en dublet af lige tal., Begivenhederne i en dublet af lige tal vil være E12 = = 3
Derfor, sandsynlighed ofgetting ‘en dublet af lige tal”
Antallet af gunstige udfald
P(E12) = det Samlede antal mulige udfald
= 3/36
= 1/12
(xiii) at få amultiple af 2 på en dør og et multiplum af 3 på den anden dør:
Lad E13 = begivenhed for at få et multiplum af 2 på en dør og et multiplum af 3 på den anden dø., Begivenhederne, der er et multiplum af 2 på en dør og et multiplum af 3 på den anden dør vil være E13 = = 11
Derfor, sandsynlighed ofgetting ‘et multiplum af 2 på en dør og et multiplum af 3 på den anden dør”
Antallet af gunstige udfald
P(E13) = det Samlede antal mulige udfald
= 11/36
4. Todice er kastet. Find (i) odds for at få summen 5, og (ii) theodds imod at få summen 6.
løsning:
Vi ved, at i en enkelt kastet af to matricer, det samlede antalaf mulige resultater er (6 6 6) = 36.
Lad S være prøvepladsen. Derefter n (s) = 36.,
(i) Oddsene for at få summen 5:
lad E1 være tilfældet med at få summen 5. Så,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Derfor, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ odds for E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) oddsene mod at få summen 6:
lad E2 være tilfældet med at få summen 6. Så,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Derfor, P(E2) = n(E2)/n(S) = 5/36
⇒ odds imod E2 = /S(E2) = (1 – 5/36)/(5/36) = 31/5.
5., To terninger, en blå og en orange, rulles samtidigt. Find sandsynligheden for at få
(i) lige tal på begge
(ii) to tal, der vises på dem, hvis sum er 9.,
Løsning:
De mulige udfald er
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
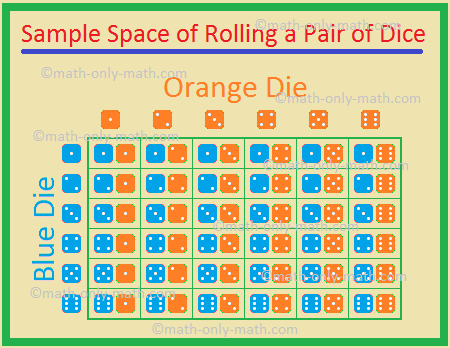
Derfor, det samlede antal af mulige udfald = 36.,
(i) antal gunstige udfald for begivenheden E
= antal udfald med samme antal på begge terninger
= 6 .
Så, per definition, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Antallet af gunstige udfald for hændelsen F
= Antallet af resultater, hvor to numre, der optræder på dem, har summen 9
= 4 .definition P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
disse eksempler vil hjælpeos til at løse forskellige typer problemer baseret på Sandsynlighed for rollingto terninger.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Skriv et svar