Når vinklerne i en trekant ikke tilføjer op til 180 grader

1. Introduktion

tilføjer vinklerne i en trekant op til 180 grader eller $\pi$ radianer? Svaret er ‘nogle gange ja, nogle gange nej’. Er dette et vigtigt spørgsmål? Ja, fordi det fører til en forståelse af, at der er forskellige geometrier baseret på forskellige aksiomer eller ‘regler for geometriens spil’. Er det et meningsfuldt spørgsmål? Nå nej, i det mindste ikke før vi er enige om betydningen af ordene ‘vinkel’ og’ Trekant’, ikke før vi kender spillereglerne., I denne artikel diskuterer vi kort de underliggende aksiomer og giver et simpelt bevis på, at summen af vinklerne i en trekant på overfladen af en enhedssfære ikke er lig med $\pi$ men til $\pi$ plus arealet af trekanten. Vi skal bruge det faktum, at arealet af overfladen af en enhed sfære er $4\pi$.

2. Den Store sætning

før vi kan sige, hvad en trekant er, er vi nødt til at blive enige om, hvad vi mener med punkter og linjer. Vi arbejder på sfærisk geometri (bogstaveligt talt geometri på overfladen af en kugle)., I denne geometri rummet er overfladen af kuglen; punkterne er punkter på denne overflade, og den linje af korteste afstand mellem to punkter er den store cirkel, der indeholder de to punkter. En stor cirkel (somækvator) skærer kuglen i to lige halvkugler. Denne geometri har indlysende anvendelser til afstande mellem steder og luftruter på jorden.,

Roterende kugle, der viser stor cirkel

vinklen mellem to store cirkler er på et punkt, P, er den Euklidiske vinkel mellem de retninger af cirkler (eller strengt mellem tangenter til cirkler på P). Dette giver ingen vanskeligheder med at navigere på jorden, fordi vi på et givet tidspunkt tænker på vinklen mellem to retninger, som om Jorden var flad på det tidspunkt.

en lune er en del af overfladen af kuglen afgrænset af to store cirkler, der mødes på antipodale punkter., Vi betragter først området med en lune og introducerer derefter en anden stor cirkel, der opdeler lune i trekanter.

Roterende kugle, der viser 4 lunes

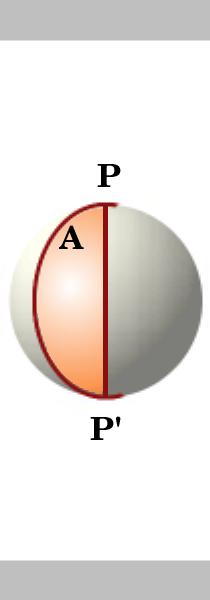
Lemma.

arealet af en lune på en cirkel af enhed radius er dobbelt sin vinkel, det vil sige, hvis vinklen af lune er en derefter sit område er 2A. to store cirkler skærer på antipodale punkter P og P’ opdele kuglen i 4 lunes. Arealet af overfladen af en enhed sfære er $4\pi$.,

De områder af lunes i forhold til deres vinkler på P, så arealet af et lune med vinkel A er

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Øvelse 1.

Hvad er områderne i de andre 3 lunes? Har dine 4 områder tilføje op til $ 4 \ pi$?

Tjek dine svar her .siderne af en trekant ABC er segmenter af tre store cirkler, der faktisk skærer kuglens overflade i otte sfæriske trekanter. Mellem de to store cirkler gennem punkt A er der fire vinkler., Vi mærker den vinkel inde i trekant ABC som En vinkel, og tilsvarende for de andre vinkler i trekant ABC som vinkel B og vinkel C.

Roterende kugle, der viser, 8 trekanter

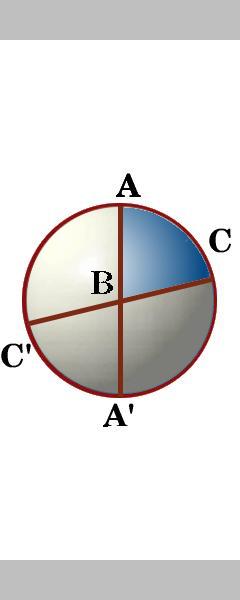
Øvelse 2

Roterende kugle kan du nævne de otte trekanter og sige, om nogen af dem har det samme område? Tjek dine svar her .

sætning.

overvej en sfærisk trekant ABC på enhedssfæren med vinkler A, B og C. Derefter er området med trekant ABC

a + b + c – $\pi$.,

diagrammet viser en visning, der ser ned på halvkuglen, som har linjen gennem AC som sin grænse. Områderne markeret med Område 1 og område 3 er mandag med henholdsvis vinkel A og C. Overvej lunes gennem B og B’. Trekant ABC er kongruent til trekant A ‘B’ C ‘så Butterfly formet skraverede område, markeret Område 2, som er summen af de områder af trekanter ABC og A’BC’, er lig med thearea af lune med vinkel B, der er lig med 2B.,

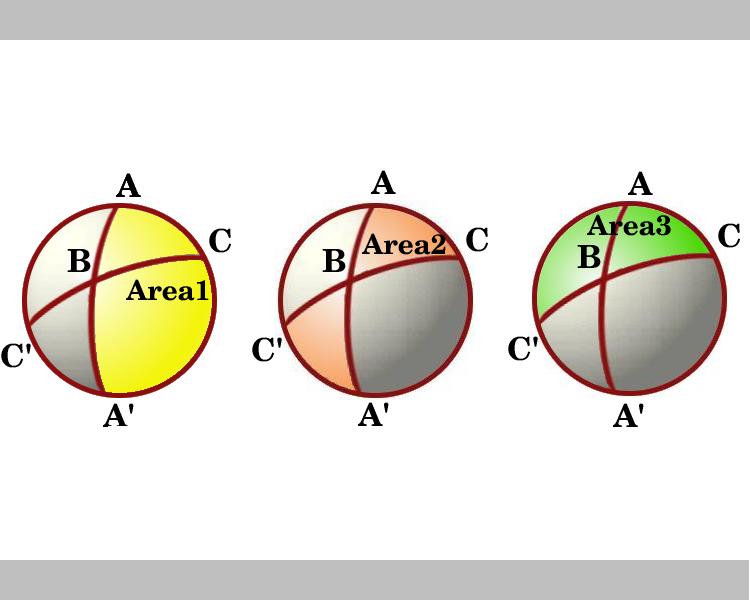
Så i diagrammet ser vi de områder, der er af tre lunes og, ved hjælp af lemma, disse er:

Område 1 = 2A
Område 2 = 2B
Område 3 = 2C

I sammenfattet disse tre områder, vi omfatter arealet af trekant ABC tre gange., Hence

3., Ikke-euklidisk geometri

Nogle gange er revolutionerende opdagelser intet andet end faktisk at se, hvad der har været under vores næser hele tiden. Dette var tilfældet i løbet af opdagelsen af ikke-euklidisk geometri i det nittende århundrede. For nogle 2000 år efter Euclid skrev hans ‘Elements’ i 325 F.kr. folk forsøgte at bevise den parallelle postulat som en sætning i geometri fra de andre aksiomer, men altid mislykkedes, og thatis en lang historie., I mellemtiden matematikere brugte sfærisk geometri hele tiden, en geometri, som adlyder de andre aksiomer af euklidisk geometri og indeholder mange af de samme teoremer, men hvor den parallelle postulat ikke holder. Alle sammen havde de et eksempel på en ikke-euklidisk geometri under deres næser.

tænk på en linje l og et punkt P ikke på L. Det store spørgsmål er: “hvor mange linjer kan tegnes gennem P parallelt med L?”I euklidisk geometri er svaret “nøjagtigt en”, og dette er en version af det parallelle postulat., Hvis summen af vinklerne i hver trekant i geometrien er $\pi$ radianer, holder det parallelle postulat og omvendt, de to egenskaber er ækvivalente.

i sfærisk geometri er de grundlæggende aksiomer, som vi antager (spillereglerne), forskellige fra euklidisk geometri – dette er en ikke-euklidisk geometri. Vi har set, at vinklerne på trekanter i sfærisk geometri ikke altid tilføjer op til$ \ pi $ radianer, så vi ville ikke forvente, at det parallelle postulat holder., I sfærisk geometri er de lige linjer (linjer med korteste afstand eller geodesik)store cirkler, og hver linje i geometrien skærer hver anden linje i to punkter. Svaret på det store spørgsmål om paralleller er`hvis vi har en linje L og et punkt P ikke på L, er der ingen linjer gennem P parallelt med linjen L.,”

Den græske matematikere (for eksempel Ptolemæus c 150) beregnet på grundlag af målinger af retvinklet sfærisk trekant og arbejdet med formler i sfærisk trigonometri, og de Arabiske matematikere (for eksempel Jabir ibn Aflah k 1125 og Nasir ed-din 1250 c) udvidet arbejde endnu mere. Formlen drøftet i denne artikel blev opdaget af Harriot i 1603 og offentliggjort af Girard i 1629. Yderligereideer af emnet blev udviklet af Saccerhi (1667 – 1733).,

alt dette gik stort set ikke bemærket af det 19.århundrede opdagere af hyperbolsk geometri, hvilket er en anden ikke-euklidisk geometri, hvor det parallelle postulat ikke holder. I sfærisk geometri (også kaldet elliptisk geometri) vinklerne af trekanter tilføje op til mere end $\pi$ radianer og i hyperbolsk geometri vinklerne af trekanter tilføje op til mindre end $\pi$ radianer.for yderligere læsning se artiklen af Alan Beardon ‘ hvor mange geometrier er der?’og artiklen af Keith Carne ‘Strange Geometries’., Der er nogle praktiske aktiviteter, som du selv kan prøve at udforske disse geometrier yderligere, der findes på http://nrich.maths.org/MOTIVATE/conf8/index.html