mænd. Jeg føler på en eller anden måde, at jeg kan lide det, du siger.
Soc. Og jeg, Meno, kan lide det, jeg siger.
fra Platons Meno
længden af diagonalen af enhedens firkant er lig med kvadratroden af 2.
længden af diagonalen af enhedens firkant er lig med 2 2. Nå, det er ikke rigtig gode nyheder. Enhver, der nogensinde stødte på Pythagoras sætning, er opmærksom på det faktum., I den enslige højre trekant med benene med længde 1 er hypotenusen ifølge Pythagoras sætning-12 + 12 = (hypotenuse)2 – Faktisk af længde 2 2. Motivationen for denne side er ikke så meget, at selve faktum, men den måde at vise det uden anvendelse af den berømte sætning. Faktisk kunne det hævdes, at Pythagoras sætning kunne have været overbrugt, se et nysgerrig eksempel.
et argument, der går tilbage til figuren tegnet af Socrates i Platons Meno, kunne have været kendt af Pythagoras selv, selvom sidstnævnte levede et århundrede tidligere.,
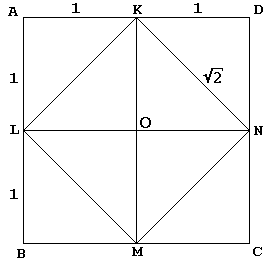
I den dialogboks, Socrates, i sin sædvanlige måde, som fører en ung slave til en konstruktion af et kvadrat, som to gange arealet af den givne en:
i betragtning af pladsen KLMN med centrum O er første cut af dens diagonaler i 4 lige store trekanter. Socrates integrerer KLMN i en større firkant ABCD som om afspejler disse trekanter hver i sin hypotenuse. Så indrømmer Trællen – og hvem ville ikke? – den firkantede ABCD er dobbelt så stor som firkantet KLMN.
sandheden skal frem, Sokrates’ kvadrat ABCD målt 4 på siden, således at kvadrat KLMN havde areal på 8., Det er klart, at når vi starter med den firkantede ABCD på side 2 (og dermed af område 4), vil firkantet KLMN have et areal på 2.
nu er generelt for et positivt tal a defined a defineret som et tal, hvis firkant er A:
(2 a)2.
På den anden side, hver elev af områder kender, at arealet af et kvadrat af side b er lig med b2. Det følger derefter, at siden af en firkant med Område A er nøjagtigt A. A. vi konkluderer, at siden af firkanten KLMN er lig med 2 2. For en,
KN=. A.
argumentets centrale punkt er det faktum, at KN i diagrammet spiller en dobbelt rolle., Udover at være en af siderne af firkantet KLMN, fungerer det også som en diagonal af firkantet OKDN. Sidstnævnte er selvfølgelig en enhed firkant, som beviser vores påstand.
(fra et lidt andet perspektiv nævnes den samme episode andetsteds.)
















Skriv et svar