Trekant Figur Vinkel-Side-Vinkel (ASA)
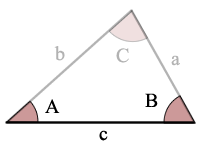
A = vinkel A
B = vinkel B
C = vinkel C
en = en
b = b-side
c = side; c
S = omkredsen
s = semi-perimeter
K = – området
r = radius af den indskrevne cirkel
R = radius af omskrevne cirkel
Regnemaskine Brug
Hver beregning indstilling, der er vist nedenfor, har sub-kugler, der viser sekvens af metoder, der er anvendt i denne regnemaskine til at beregne ukendte vinkel-og side-værdier, der omfatter Summen af Vinklerne i en Trekant, i Lov af Sines og Lov om Hygge., Dette er ikke de eneste sekvenser, du kan bruge til at løse disse typer problemer.
- Se også disse Trigonometri Regnemaskiner:
- Lov af Hygge Regnemaskine
- Lov for Sines Regnemaskine
Løsning Trekant Teoremer
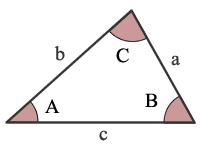
AAA er vinkel, Vinkel, Vinkel
Angivelse af de tre vinkler i en trekant ikke entydigt at identificere en trekant. Derfor angiver to vinkler af en tringle dig kun at beregne den tredje vinkel.,
i betragtning af størrelserne på 2 vinkler i en trekant kan du beregne størrelsen på den tredje vinkel. Den samlede vil være lig med 180 or eller radi radianer.
C = 180° – A – B (i grader)
C = π – A – B (i radianer)
AAS vinkel, Vinkel, Side
i Betragtning af størrelsen af 2 vinkler og 1 modsatte side, af en af de givne vinkler, kan du beregne størrelsen af de resterende 1 vinkel og 2 sider.
brug summen af vinkler til at finde den anden vinkel, og brug derefter Sines-loven til at løse for hver af de to andre sider.,
ASA er vinkel, side, vinkel
i betragtning af størrelsen på 2 vinkler og størrelsen på den side, der er mellem disse 2 vinkler, kan du beregne størrelserne på den resterende 1 vinkel og 2 sider.
brug summen af vinkler til at finde den anden vinkel, og brug derefter Sines-loven til at løse for hver af de to andre sider.,
ASS (eller SSA) er Vinkel, Side, Side
i Betragtning af størrelsen af 2 sider, litra a og c, hvor a < c), og størrelsen af En vinkel, som ikke er i mellem disse 2 sider, du måske være i stand til at beregne størrelser af de resterende side 1 og 2 vinkler, afhængigt af de følgende betingelser.,f Cosinus til at løse for hver af de to andre vinkler
nuværende 2 komplette løsninger
Eksempel: 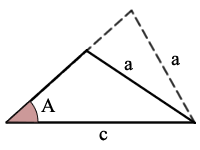
sin(A) = a/c, der er en mulig trekant
brug Den Lov, i Sines for at finde en vinkel, C
brug Summen af Vinklerne Regel at finde en anden vinkel, B
brug Den Lov, i Sines for at finde den sidste side, b
Eksempel: 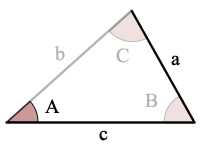
sin(A) > a/c, der er ingen mulige trekanter
Fejl Meddelelse: sin(A) > a/c, så der er ingen løsninger og ingen trekant!,
Eksempel: 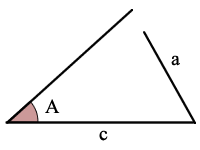
SAS Side, Vinkel, Side
i Betragtning af størrelsen af 2 sider (c og a), og størrelsen af vinkel B, der er i mellem disse 2 sider kan du beregne størrelsen af de resterende side 1 og 2 vinkler.
brug cosinus-loven til at løse for den resterende side bestemmer b
hvilken side, a eller c, der er mindste, og brug Sines-loven til at løse for størrelsen af den modsatte vinkel, henholdsvis A eller C.,
brug summen af vinkler til at finde den sidste vinkel
SSS er Side, Side, Side
i betragtning af størrelserne på de 3 sider kan du beregne størrelserne på alle 3 vinkler i trekanten.
brug cosinus lov til at løse for vinklerne. Du kan også bruge summen af vinkler regel at finde den endelige vinkel, når du kender 2 af dem.,sin-1
Lov af Hygge
Hvis a, b og c er længden af benene af en trekant overfor at vinklerne A, B og C henholdsvis; derefter lov af hygge hedder det:
a2 = c2 + b2 – 2bc cos A, løse for cos A cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, løse for cos B cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, løse for cos C cos C = ( a2 + b2 – c2 ) / 2ab
Løsning, for eksempel, til en vinkel, A = cos-1
Andre Trekant Egenskaber
Trekant omkreds, P = a + b + c
Trekant semi-perimeter, s = 0.,5 * (a + b + c)
Trekant-området, K = √
Radius af den indskrevne cirkel i trekant, r = √
Radius af omskrevne cirkel, trekant, R = (abc) / (4K)
Referencer/ Yderligere Læsning
Weisstein, Eric W. “RØV Sætning.”Fra Math .orld-En Resourceolfram Resourceebressource . Røv sætning.
matematik er sjovt at løse SAS-trekanter
















Skriv et svar