konvekse og konkave polygoner

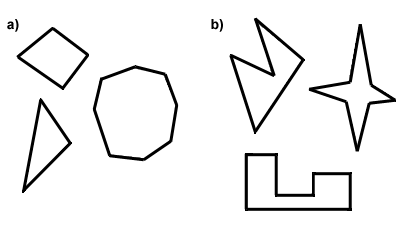
hver polygon er enten konveks eller konkav. Denforskellen mellem konvekse og konkave polygoner ligger i målene for deres vinkler. For en polygon at værekonveks, skal alle dets indvendige vinkler være mindre end 180 grader. Ellers er polygonenconcave. En anden måde at tænke på det er dette: diagonalerne i en conve .polygon vil alle være i det indre af polygonen, mens visse diagonaler af en konkav polygon vil ligge uden for polygonen på dens ydre., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

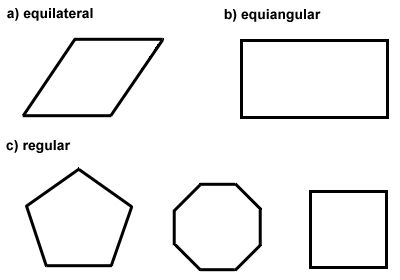
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Når en polygon er både ligesidet og e .uiangular, kaldes det en regelmæssig polygon. En firkant er et eksempel på en regelmæssig polygon. Midten af en regelmæssig polygon er det punkt, hvorfra alle polygonens hjørner er ens. Regelmæssige polygoner har særlige egenskaber, som vi vil udforske i næste afsnit. Nedenfor er nogle eksempler på e .uiangular, ligesidede og regulære polygoner.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.