Gennemsnit, Median, Mode: Hvad De Er, Hvordan at Finde Dem

Indhold (Klik for at springe til det pågældende afsnit):

1. Alt om det…
   • Betyde
   • Mode
   • Median
2. Hvordan til at finde ud af gennemsnit, median og modus ved hånden.
3. Find middelværdien, medianen og tilstanden med teknologi:
   • SPSS
   • TI83

oversigt

sidder fast på, hvordan man finder middelværdien, medianen,& tilstand i statistik?,

1. gennemsnittet er gennemsnittet af et datasæt.
2. tilstanden er det mest almindelige tal i et datasæt.
3. medianen er midten af sættet af tal.

af de tre er middelværdien den eneste, der kræver en formel. Jeg kan godt lide at tænke på det i den anden ordbogssans af ordet (som i, det er middel i modsætning til nice!). Det er fordi, sammenlignet med de to andre, det er ikke så let at arbejde med.,

tip til at huske forskellen

Har du problemer med at huske forskellen mellem middel, median og tilstand? Her er et par tip, der kan hjælpe. Du kan også tjekke vejledere på Chegg.com (dine første 30 minutter er gratis!).

• “a la mode” er et fransk ord, der betyder moderigtigt ; det henviser også til en populær måde at servere is på. Så “Mode” er det mest populære eller fashionable medlem af et sæt tal. Ordet tilstand er også som de fleste.,
• den ” gennemsnitlige “kræver, at du laver aritmetik (tilføjer alle tal og deler), så det er den” gennemsnitlige”.
• “Median “har det samme antal bogstaver som”midten”.

er du stadig ikke sikker på, hvad forskellen er mellem de tre? Se videoen eller læs videre for mere info:

middel

middel vs. Median
middel vs., Gennemsnitlig
Særlige “Middel”, der almindeligvis anvendes i Statistik
Andre Typer

Betyder vs Median

Både er tale om, hvor midten af et datasæt ligger (kaldet “Central Tendens” i statistik), men de er som regel forskellige numre. Tag for eksempel denne liste over tal: 10, 10, 20, 40, 70.

• middelværdien (uformelt “gennemsnittet”) findes ved at tilføje alle tallene sammen og dividere med antallet af elementer i sættet: 10 + 10 + 20 + 40 + 70 / 5 = 30.
• medianen findes ved at bestille sættet fra laveste til højeste og finde den nøjagtige midten., Medianen er kun det midterste tal: 20.

Nogle gange vil de to være det samme nummer. For eksempel har datasættet 1, 2, 4, 6, 7 et gennemsnit af 1 + 2 + 4 + 6 + 7 / 5 = 4 og en median (en midten) på 4.

middel vs gennemsnit: Hvad er forskellen?

da du først startede i matematik, blev du sandsynligvis lært, at et gennemsnit var et “middel” beløb for et sæt tal. Du har tilføjet op numrene, divideret med antallet af emner, du kan og voila! du får gennemsnittet. For eksempel er gennemsnittet på 10, 5 og 20:

10 + 6 + 20 = 36 / 3 = 12.,

du begyndte at studere statistik, og pludselig kaldes “gennemsnittet” nu middelværdien. Hvad skete der? Svaret er, at de har samme betydning(de er synonymer).

når det er sagt, er ordet teknisk set kort for det aritmetiske gennemsnit. Vi bruger forskellige ord i statistik, fordi der er flere forskellige typer midler, og de gør alle forskellige ting.

specifikke “midler”, der ofte bruges i statistik

Du vil sandsynligvis støde på disse i din statistikklasse., De har meget snævre betydninger:

• middelværdi af prøveudtagningsfordelingen: bruges med sandsynlighedsfordelinger, især med den centrale grænsesætning. Det er et gennemsnit af et sæt distributioner.
• Sample middelværdi: gennemsnitsværdien i en prøve.
• Populationsmiddelværdi: gennemsnitsværdien i en population.

Kenney, J. F. og Holde, E. S. Matematik Statistik, Pt. 1, 3.udgave. Princeton, NJ: Van Nostrand, 1962.

andre typer

Der er andre typer midler, og du vil bruge dem i forskellige grene af matematik., De fleste har meget smalle applikationer til felter som finansiering eller fysik; hvis du er i elementær statistik, vil du sandsynligvis ikke arbejde med dem.

Dette er nogle af de mest almindelige typer, du vil støde på.

1. vægtet gennemsnit.
2. harmonisk middelværdi.
3. Geometrisk middelværdi.
4. aritmetisk-Geometrisk middelværdi.
5. Root-Mean s .uare mean.
6. Heronian middelværdi.
7. Grafisk gennemsnit

1. vægtet gennemsnit

   disse er ret almindelige i statistikker, især når man studerer populationer., I stedet for at hvert datapunkt bidrager ligeligt til det endelige gennemsnit, bidrager nogle datapunkter mere end andre. Hvis alle vægte er ens, vil dette svare til det aritmetiske gennemsnit. Der er visse omstændigheder, når dette kan give forkerte oplysninger, som det fremgår af Simpsons paradoks.

2. Harmonic Mean

   

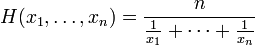
   Den harmoniske formel.

   for at finde det:

   1. Tilføj reciprocals af tallene i sættet., For at finde en gensidig, vend fraktionen, så tælleren bliver nævneren, og nævneren bliver tælleren. For eksempel er den gensidige af 6/1 1/6.
   2. del svaret med antallet af elementer i sættet.
   3. tag det gensidige af resultatet.

   det harmoniske middel bruges ganske meget i fysikken. I nogle tilfælde involverer satser og nøgletal det giver et bedre gennemsnit end det aritmetiske gennemsnit. Du finder også anvendelser inden for geometri, Økonomi og datalogi.,

3. geometrisk gennemsnit

   
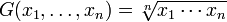
   denne type har meget snævre og specifikke anvendelser inden for økonomi, samfundsvidenskab og teknologi. For eksempel, lad os sige, at du ejer aktier, der tjener 5% det første år, 20% det andet år og 10% det tredje år. Hvis du vil vide den gennemsnitlige afkast, kan du ikke bruge det aritmetiske gennemsnit. Hvorfor? Fordi når du finder afkast, multiplicerer du, ikke tilføjer. For eksempel multiplicerer du det første år med 1,05.,

4. aritmetisk-geometrisk gennemsnit

   Dette bruges mest i beregning og i maskinberegning (dvs.som grundlæggende for mange computerberegninger). Det er relateret til omkredsen af en ellipse. Da den først blev udviklet af Gauss, blev den brugt til at beregne planetariske baner. Den aritmetiske-geometriske er (ikke overraskende!) en blanding af det aritmetiske og geometriske gennemsnit. Matematikken er ret kompliceret, men du kan finde en relativt enkel forklaring på matematikken her.,

5. root-Mean s .uare

   det er meget nyttigt inden for områder, der studerer sinusbølger, som Elektroteknik. Denne særlige type kaldes også det kvadratiske gennemsnit. Se: Kvadratisk Middel / Rod Middel Firkant.

6. Heronian middel

   anvendt i geometri til at finde volumenet af en pyramidal frustum. En pyramidal frustum er dybest set en pyramide med spidsen skåret af.

7. Grafisk gennemsnit

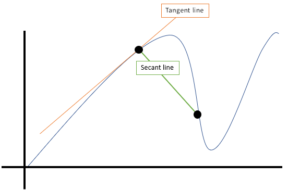
   et andet navn for skråningen af sekantlinjen: ækvivalenten af den gennemsnitlige ændringshastighed mellem to punkter.,
   

Hvad er tilstanden?

tilstanden er det mest almindelige tal i et sæt. For eksempel er tilstanden i dette sæt tal 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33

Hvad er medianen?

medianen er det midterste tal i et datasæt. For at finde medianen skal du liste dine datapunkter i stigende rækkefølge og derefter finde det midterste nummer., Det midterste tal i dette sæt er 28, da der er 4 numre under det, og 4 tal frem:
23, 24, 26, 26, 28, 29, 30, 31, 33

Hvordan til at finde ud af gennemsnit, median og modus ved hånden: Trin

Hvordan til at finde ud af gennemsnit, median og modus: MODE

Hvordan til at finde ud af gennemsnit, median og modus: BETYDE

Dividere summen med antallet af elementer, for at finde den betyder.

Sådan finder du middelværdi, median og tilstand: MEDIAN

Hvis du havde et ulige tal i trin 3, skal du gå til trin 5. Hvis du havde et lige tal, skal du gå til trin 6.,tip: du kan have mere end .n tilstand. For eksempel er tilstanden af 1, 1, 5, 5, 6, 6 til 1, 5 og 6.

ligesom forklaringen? Tjek praktisk Snyd statistik håndbog, som har hundredvis flere trin-for-trin-løsninger, ligesom denne ene!

SPSS Middeltilstand median

for at finde SPSS middeltilstand median, skal du bruge fanen frekvens. Det virker lidt modintuitivt, men fanen Beskrivende statistik giver dig ikke muligheden for at finde tilstanden eller medianen.,

SPSS har en meget lignende grænseflade til Microsoft e .cel. Derfor, hvis du har brugt Microsoft e .cel før, vil du hurtigt tilpasse dig SPSS.

SPSS Middeltilstand Median: trin

se videoen eller læs nedenstående trin:

prøve spørgsmål: Find SPSS middeltilstand median for følgende datasæt: 20,23,35,66,55,66

Trin 1: Åbn SPSS. I “hvad vil du gerne gøre?”dialogboks, klik på alternativknappen” type in data “og klik derefter på” OK.”Et nyt regneark åbnes., Bemærk: Hvis du har fravalgt den første hjælpeskærm, kan du muligvis ikke se denne mulighed. I så fald skal du bare starte ved Trin 2.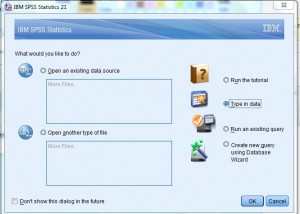

Trin 2: Indtast dine data i regnearket. Du kan indtaste dataene i en kolonne eller flere kolonner, hvis du har flere datasæt. For dette eksempel skal du skrive 20, 23, 35, 66, 55, 66 i kolonne 1. Efterlad ikke mellemrum mellem dataene (dvs.Efterlad ikke tomme rækker).trin 2: Klik på “Analyser”, hold markøren over” Beskrivende statistik”, og klik derefter på ” frekvenser.,”

Trin 3: Klik på” statistik”, og marker derefter afkrydsningsfelterne” middel”,” tilstand “og” median.”Klik” Fortsæt “to gange (Vælg” ingen ” som diagramtype i det andet vindue).bemærk: i nogle versioner af SPSS skal du muligvis kun klikke på” Fortsæt ” oncen gang, og det giver dig muligvis ikke en mulighed for diagramtype.

frekvensresultaterne vises som output. Den øverste del af output vil vise middelværdi, tilstand og median.

Hvis du ruller ned, viser frekvenstabellen dig også tilstanden., Tilstanden er defineret i statistikken som det tal med den højeste frekvens (for denne prøve datasæt, det tal, der vises mest er 66, med to resultater i kolonnen frekvens).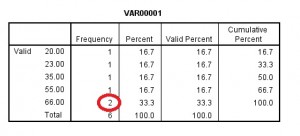

TI 83 middel, Median og Mode

find TI 83 middel eller TI 83 median fra en liste over data kan udføres på to måder: ved at indtaste en liste over data eller ved at bruge startskærmen til at skrive kommandoerne., Brug af listefunktionen er lige så let som at indtaste dataene på startskærmen, og det har den ekstra fordel, at du kan bruge dataene til andre formål, efter at du har beregnet din middelværdi, tilstand og median (for eksempel kan du oprette et TI 83-histogram).

Trin for Middelværdi, Median og Modus på TI 83

Se video for middelværdi og median, eller læs trin nedenunder (for den tilstand, skal du se denne note):