En vektor har en størrelse (hvor langt det er) og ledelse:
Her er to vektorer:

De kan blive mangedoblet ved hjælp af “Dot-Produkt” (se også på Tværs af Produkt).,
Vi kan beregne Prik-Produktet af to vektorer på denne måde:

a · b = |a| x |b| × cos(θ)
Hvor:
|a| er størrelsen (længde) af en vektor
|b| er størrelsen (længden) af vektor b
θ er vinklen mellem a og b
Så vi ganger længden af en gange længden af b, og derefter multipliceres med cosinus af vinklen mellem a og b
, ELLER vi kan beregne det på denne måde:
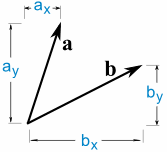
a · b = ax x bx + ay × ved
Så vi ganger x ‘er, skal du gange den y’, klik derefter på add.,
begge metoder virker!
og resultatet er et tal (kaldet en “skalar”, så vi ved, at det ikke er en vektor).
Bemærk: Du kan bruge Vektorberegningenfor at hjælpe dig.
hvorfor cos ())?
OK, for at multiplicere to vektorer er det fornuftigt at multiplicere deres længder sammen, men kun når de peger i samme retning.,
Så vi laver et “peger i samme retning” som den anden ved multiplikation med cos(θ):
 |
 |
|
| Tager vi den del af en der ligger sammen med b |
Som skinner et lys at se, der, hvor skyggen løgne |
SÅ vi ganger !,
rette vinkler
Når to vektorer er vinkelret på hinanden, er prikproduktet nul.
dette kan være en praktisk måde at finde ud af, om to vektorer er i rette vinkler.
tre eller flere dimensioner
alt dette fungerer fint i 3 (eller flere) dimensioner også.
og kan faktisk være meget nyttigt!
Jeg prøvede en sådan beregning en gang, men arbejdede alle i vinkler og afstande … det var meget hårdt, involverede masser af trigonometri, og min hjerne gjorde ondt. Metoden ovenfor er meget lettere.,
krydsprodukt
Prikproduktet giver et skalært (almindeligt antal) svar og kaldes undertiden det skalære produkt.
men der er også Krydsproduktet, der giver en vektor som svar, og kaldes undertiden vektorproduktet.

















Skriv et svar