Vis Mobile Varsel Vis Alle Noter Skjule Alle Noter
afsnit 4-11 : lineære tilnærmelser
i dette afsnit vil vi se på en applikation ikke af derivater, men af tangentlinjen til en funktion. For at få tangentlinjen er vi selvfølgelig nødt til at tage derivater, så på en eller anden måde er dette også en anvendelse af derivater.
\
Tag et kig på følgende graf af en funktion og dens tangent linje.
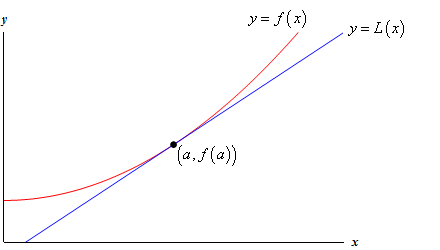
så hvorfor skulle vi gøre dette? Lad os tage et kig på et eksempel.,
lineære tilnærmelser gør et meget godt stykke arbejde med at tilnærme værdier af \(f\venstre (\\højre)\), så længe vi forbliver “nær”\(. = a\). Men jo længere væk fra \(==A\) bliver vi værre tilnærmelsen er tilbøjelig til at være. Det største problem her er, at hvor tæt vi har brug for at blive til \(==A\) for at få en god tilnærmelse afhænger af både den funktion, vi bruger, og værdien af \(. = A\), som vi bruger. Der vil også ofte ikke være nogen nem måde at forudsige, hvor langt væk fra \(==A\) Vi kan få og stadig have en “god” tilnærmelse.,
lad os se på et andet eksempel, der faktisk bruges temmelig tungt nogle steder.
Dette er faktisk en noget vigtig lineær tilnærmelse. I optik bruges denne lineære tilnærmelse ofte til at forenkle formler. Denne lineære tilnærmelse bruges også til at beskrive bevægelsen af et pendul og vibrationer i en streng.
















Skriv et svar