Vis Mobile Varsel Vis Alle Noter Skjule Alle Noter
Afsnit 3-1 : Parametriske Ligninger og Kurver
Til dette punkt (i både Calculus i og Calculus II) vi har kigget næsten udelukkende på funktioner i form \(y = f\left( x \right)\) eller \(x = t\left( y \right)\), og næsten alle af de formler, som vi har udviklet, kræver, at funktioner være i en af disse to former. Problemet er, at ikke alle kurver eller ligninger, som vi gerne vil se på, falder let i denne form.
tag for eksempel en cirkel. Det er let nok at skrive ned ligningen for en cirkel centreret ved oprindelsen med radius \(r\).,
\
vi vil dog aldrig være i stand til at skrive ligningen for en cirkel ned som en enkelt ligning i en af ovenstående former. Sikker på, at vi kan løse for \(\ \ ) eller \(y\), da de følgende to formler viser
\
, men der er faktisk to funktioner i hver af disse. Hver formel giver en del af cirklen.
\
desværre arbejder vi normalt på hele cirklen, eller kan simpelthen ikke sige, at vi kun vil arbejde på en del af det. Selvom vi kun kan indsnævre tingene til en af disse dele, er funktionen stadig ofte temmelig ubehagelig at arbejde med.,
\
denne tredje variabel er normalt betegnet med \(T\) (som vi gjorde her), men behøver ikke at være selvfølgelig. Nogle gange vil vi begrænse værdierne af \(T\), som vi vil bruge, og på andre tidspunkter vil vi ikke. dette vil ofte være afhængig af problemet og lige hvad vi forsøger at gøre.
for at hjælpe med at visualisere, hvad en parametrisk kurve er, foregive at vi har en stor vandtank, der er i konstant bevægelse, og vi slipper en ping pong-bold ind i tanken., Punktet \(\venstre ({,, y} \højre) = \venstre( {f\venstre( t \højre), g\venstre( t \højre)} \højre)\) repræsenterer derefter placeringen af ping pong-kuglen i tanken på time \(t\), og den parametriske kurve vil være et spor af alle placeringer af ping pong-kuglen. Bemærk, at dette ikke altid er en korrekt analogi, men det er oprindeligt nyttigt at hjælpe med at visualisere, hvad en parametrisk kurve er.
skitsering af en parametrisk kurve er ikke altid en nem ting at gøre. Lad os tage et kig på et eksempel for at se en måde at skitsere en parametrisk kurve på., Dette eksempel vil også illustrere, hvorfor denne metode normalt ikke er den bedste.eksempel 1 skitser den parametriske kurve for følgende sæt parametriske ligninger. \
På dette tidspunkt er vores eneste mulighed for at skitsere en parametrisk kurve at vælge værdier af \(t\), sætte dem i de parametriske ligninger og derefter plotte punkterne. Så lad os tilslutte nogle \(T\) s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Desværre er der ikke noget reelt svar på dette spørgsmål på dette tidspunkt. Vi vælger simpelthen \(t\), indtil vi er ret sikre på, at vi har en god ide om, hvordan kurven ser ud. Det er dette problem med at vælge “gode” værdier af \(T\), der gør denne metode til at skitsere parametriske kurver til et af de dårligere valg. Nogle gange har vi ikke noget valg, men hvis vi har et valg, bør vi undgå det.
Vi vil diskutere en alternativ graftegning metode i senere eksempler, der vil bidrage til at forklare, hvordan disse værdier af \(T\) blev valgt.,
Vi har endnu en ID.at diskutere, før vi faktisk skitserer kurven. Parametriske kurver har en bevægelsesretning. Bevægelsesretningen er givet ved at øge \(t\). Så når vi planlægger parametriske kurver, inkluderer vi også pile, der viser bevægelsesretningen. Vi vil ofte give værdien af \(T\), der også gav specifikke punkter på grafen for at gøre det klart værdien af \(T\), der gav det pågældende punkt.
Her er skitsen af denne parametriske kurve.
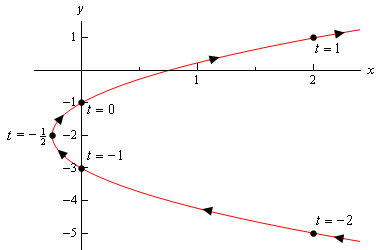
så det ser ud til, at vi har en parabola, der åbnes til højre.,
før vi afslutter dette eksempel er der et noget vigtigt og subtilt punkt, som vi først skal diskutere. Bemærk, at vi sørgede for at medtage en del af skitsen til højre for de punkter, der svarer til \(T = – 2\) og \(T = 1\) For at indikere, at der er dele af skitsen der. Havde vi simpelthen stoppet skitsen på disse punkter, indikerer vi, at der ikke var nogen del af kurven til højre for disse punkter, og der vil helt klart være. Vi har bare ikke beregne nogen af disse punkter.,
dette kan virke som et ubetydeligt punkt, men som vi ser i det næste eksempel er det vigtigere, end vi måske tror.
før vi adresserer en meget lettere måde at skitsere denne graf på, lad os først løse problemet med grænser for parameteren. I det foregående eksempel havde vi ingen grænser for parameteren. Uden grænser for parameteren vil grafen fortsætte i begge retninger som vist på skitsen ovenfor.
Vi vil dog ofte have grænser for parameteren, og dette vil påvirke skitsen af de parametriske ligninger., For at se denne effekt lad os se en lille variation af det foregående eksempel.eksempel 2 skitser den parametriske kurve for følgende sæt parametriske ligninger. \
Bemærk, at den eneste forskel her er tilstedeværelsen af grænserne for \(t\). Alle disse grænser gør, er at fortælle os, at vi ikke kan tage nogen værdi af \(T\) uden for dette interval. Derfor vil den parametriske kurve kun være en del af kurven ovenfor. Her er den parametriske kurve for dette eksempel.,
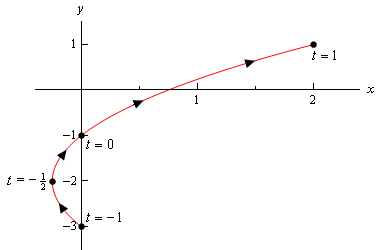
Bemærk, at med denne skitse vi startede og stoppede den skitse lige på de punkter, der stammer fra slutningen punkter af den vifte af \(t\)’s. Kontrast dette med skitsen i det foregående eksempel, hvor vi havde en del af skitsen til højre for “start” og “slut” – punkter, som vi beregnede.
i dette tilfælde starter kurven ved \(T = – 1\) og slutter ved \(T = 1\), mens kurven i det foregående eksempel ikke rigtig startede på de rigtige punkter, som vi beregnet., Vi skal være klar i vores skitser, hvis kurven starter/slutter lige på et punkt, eller hvis det punkt var simpelthen den første / sidste, som vi beregnet.
det er nu tid til at se på en lettere metode til at skitsere denne parametriske kurve. Denne metode bruger det faktum, at vi i mange, men ikke alle tilfælde, faktisk kan eliminere parameteren fra de parametriske ligninger og få en funktion, der kun involverer \(\ \) og\(y\). Vi vil undertiden kalde dette den algebraiske ligning for at differentiere den fra de oprindelige parametriske ligninger., Der vil være to små problemer med denne metode, men det vil være let at løse disse problemer. Det er dog vigtigt at bemærke, at vi ikke altid kan gøre dette.
hvordan vi eliminerer parameteren afhænger af de parametriske ligninger, vi har. Lad os se, hvordan du fjerner parameteren for det sæt parametriske ligninger, som vi har arbejdet med til dette punkt.
at få en skitse af den parametriske kurve, når vi har fjernet parameteren, virker ret simpel. Alt, hvad vi skal gøre, er at tegne ligningen, som vi fandt ved at fjerne parameteren., Som allerede nævnt er der dog to små problemer med denne metode. Den første er bevægelsesretning. Ligningen, der kun involverer \(\ \) og \ (y\), giver ikke bevægelsesretningen for den parametriske kurve. Dette er generelt et let problem at løse dog. Lad os tage et hurtigt kig på derivaterne af de parametriske ligninger fra det sidste eksempel. De er,
\
Bemærk, at \(\ \) – derivatet ikke er så nyttigt til denne analyse, da det vil være både positivt og negativt og dermed\ (\\) vil være både stigende og faldende afhængigt af værdien af \ (T\)., Det hjælper ikke med retning meget som at følge kurven i begge retninger vil udvise både stigende og faldende \(\ \ ).
i nogle tilfælde vil kun en af ligningerne, som dette eksempel, give retningen, mens i andre tilfælde enten en kunne bruges. Det er også muligt, at begge derivater i nogle tilfælde ville være nødvendige for at bestemme retning. Det vil altid være afhængig af det enkelte sæt parametriske ligninger.,
det andet problem med at eliminere parameteren illustreres bedst i et eksempel, da vi løber ind i dette problem i de resterende eksempler.
Okay, det var et rigtig langt eksempel. De fleste af disse typer problemer er ikke så længe. Vi havde lige meget at diskutere i denne, så vi kunne få et par vigtige ideer ud af vejen. Resten af eksemplerne i dette afsnit bør ikke tage så lang tid at gå igennem.lad os nu se på et andet eksempel, der illustrerer en vigtig ide om parametriske ligninger.,
så vi så i de sidste to eksempler to sæt parametriske ligninger, der på en eller anden måde gav den samme graf. Men fordi de spores grafen et andet antal gange, har vi virkelig brug for at tænke på dem som forskellige parametriske kurver i det mindste på en eller anden måde. Dette kan virke som en forskel, som vi ikke behøver at bekymre os om, men som vi vil se i senere afsnit, kan dette være en meget vigtig forskel. I nogle af de senere afsnit har vi brug for en kurve, der spores nøjagtigt en gang.,før vi går videre til andre problemer, lad os kort erkende, hvad der sker ved at ændre \(t\) til en nt i disse slags parametriske ligninger. Når vi beskæftiger os med parametriske ligninger, der kun involverer sines og cosines, og de begge har det samme argument, hvis vi ændrer argumentet fra \(T\) til nt, ændrer vi simpelthen den hastighed, som kurven spores ud med. Hvis \(n > 1\) øger vi hastigheden, og hvis \(n < 1\) reducerer vi hastigheden.
lad os tage et kig på et par flere eksempler.,
til dette punkt har vi set eksempler, der ville spore den komplette graf, som vi fik ved at fjerne parameteren, hvis vi tog et stort nok udvalg af \(T\)’S. men i det foregående eksempel har vi nu set, at dette ikke altid vil være tilfældet. Det er mere end muligt at have et sæt parametriske ligninger, som løbende vil spore kun en del af kurven. Vi kan normalt afgøre, om dette vil ske ved at kigge efter grænser for \(\ \) og\ (Y\), der pålægges os af den parametriske ligning.,
Vi vil ofte bruge parametriske ligninger til at beskrive stien til et objekt eller en partikel. Lad os se på et eksempel på det.
Vi bør give en lille advarsel på dette tidspunkt. På grund af de id .er, der er involveret i dem, vi koncentreret om parametriske kurver, der retraced dele af kurven mere end .n gang. Må ikke, imidlertid, få alt for låst ind i tanken om, at dette altid vil ske. Mange, hvis ikke de fleste parametriske kurver vil kun spore en gang. Det første, vi kiggede på, er et godt eksempel på dette. Den parametriske kurve vil aldrig gentage nogen del af sig selv.,
Der er et sidste emne, der skal diskuteres i dette afsnit, før du går videre. Indtil videre har vi startet med parametriske ligninger og elimineret parameteren for at bestemme den parametriske kurve.
Der er dog tidspunkter, hvor vi vil gå den anden vej. I betragtning af en funktion eller ligning ønsker vi måske at nedskrive et sæt parametriske ligninger for det. I disse tilfælde siger vi, at vi parametriserer funktionen.
Hvis vi tager eksempler 4 og 5 som eksempler, kan vi gøre dette for ellipser (og dermed cirkler)., I betragtning af ellipsen
\
et sæt parametriske ligninger for det ville være,
\
dette sæt parametriske ligninger sporer ellipsen,der starter ved punktet \(\venstre( {A, 0} \højre)\) og sporer i retning mod uret og sporer nøjagtigt en gang i området \(0 \le t \le 2\pi \). Dette er et ret vigtigt sæt parametriske ligninger, da det bruges kontinuerligt i nogle fag med at håndtere ellipser og/eller cirkler.
hver kurve kan parametriseres på mere end en måde. Ethvert af følgende parametriserer også den samme ellipse.,
\
tilstedeværelsen af \(\omega \) ændrer den hastighed, som ellipsen roterer, som vi så I eksempel 5. Bemærk også, at de to sidste sporer ellipser med en bevægelsesretning med uret (Du vil måske bekræfte dette). Bemærk også, at de ikke alle starter på samme sted (hvis vi tænker på \(T = 0\) som udgangspunkt).
Der er selvfølgelig mange flere parametriseringer af en ellipse, men du får ideen. Det er vigtigt at huske, at hver parameterisering sporer kurven en gang med et potentielt andet interval af \(T\)’s., Hver parameterisering kan rotere med forskellige bevægelsesretninger og kan starte på forskellige punkter.
du kan finde det Du har brug for en parameterindstilling af en ellipse, der starter på et bestemt sted, og har en særlig retning af bevægelse, og nu ved du, at noget arbejde, kan du skrive en sæt af parametriske ligninger, som vil give dig den adfærd, som du leder efter.
lad os nu skrive et par andre vigtige parametriseringer, og alle kommentarer om bevægelsesretning, udgangspunkt og rækkevidde af \(T\) for et spor (hvis relevant) er stadig sandt.,
for det første, fordi en cirkel ikke er andet end et specielt tilfælde af en ellipse, kan vi også bruge parameteriseringen af en ellipse til at få de parametriske ligninger for en cirkel centreret ved oprindelsen af radius \(r\). En mulig måde at parameterize en cirkel er,
\ \
På dette punkt er det måske ikke forekommer så nyttigt at gøre en parameterindstilling af en funktion som denne, men der er mange tilfælde, hvor det vil faktisk være nemmere, eller det kan endda være nødvendigt, at arbejde med parametrering i stedet for selve funktionen., Desværre forekommer næsten alle disse tilfælde i et Calculus III-kursus.
















Skriv et svar