I dag tager vi et kig på de mest populære valg prismodel. Black Scholes-modellen, også kendt som Black-Scholes-Merton-metoden, er en matematisk model til prisfastsættelse af optionskontrakter. Det virker ved at estimere variationen i finansielle instrumenter. Teknikken bygger på antagelsen om, at priserne følger en lognorm fordeling. Baseret på dette, det stammer værdien af en option.,

det er mere egnet til sti-uafhængige muligheder, som investorerne ikke kan udøve før deres forfaldsdato. Dette gør det anderledes end den binomiale optionsprismodel, som er en risikoneutral metode til værdiansættelse af stiafhængige muligheder (f.eks.analytikere og investorer anser Black Scholes for at være et af de væsentlige begreber i moderne finansiel teori.

der blev Indført i 1973 i Journal of Political Economy, af Fischer Black og Myron Scholes, og senere bygget af Robert Merton, model, der vandt Nobelprisen i økonomi i 1997.,

modellen følger en differentialligning, som vi bruger til at løse for optioner’ priser. Vi bruger standardvariationen af modellen til europæiske stilindstillinger. Black Scholes er ikke egnet til amerikanske stil muligheder, da det ikke anser investorer kan udøve disse muligheder på ethvert tidspunkt før deres udløbsdato.

metoden antager, at prisen på den underliggende bestand følger en lognorm fordeling, da den ikke kan være negativ. Den fordeling, som modellen er afhængig af, er baseret på Bro .nian motion, en teori til forudsigelse af naturligt forekommende tilfældige fænomener.,

Vi bruge modellen til at beregne et skøn for en mulighed, pris, med følgende oplysninger:

  • Den aktuelle pris;
  • strike-pris;
  • Tid til udløb;
  • Forventede udbytte;
  • Forventede rente; og
  • Forventede volatilitet.

i starten overvejer modellen ikke effekten af udbytteudbetalinger. Derfor er det ofte tilpasset til at gøre det ved at bestemme e.-udbytte dato værdi af det underliggende aktiv., Udbytteudbyttet har den virkning at reducere den nuværende aktiekurs, fordi optionsindehaveren forgår udbyttet.

antagelser

Black Scholes-modellen virker kun, hvis vi tager visse antagelser.,s opstå under den mulighed levetid (dette var en antagelse i den oprindelige model, som analytikere har da elimineret ved at tilføje udbytte i modellen formel);

  • markederne er helt effektiv, hvilket betyder, at vi ikke kan forudsige deres bevægelser;
  • Køb og salg af optioner indebærer ingen transaktionsomkostninger;
  • Både volatiliteten af det underliggende aktiv og den risikofri rente er konstant, indtil den udløbsdato, der er ikke korrekt, som i virkeligheden volatilitet skift med udbud og efterspørgsel, og

  • afkastet af det underliggende aktiv følger en normal fordeling.,

    • Black Scholes formel

    modelformlen er ret kompleks matematisk, hvilket ikke er et bestemt problem, da vi kan anvende specialiserede værktøjer til at beregne det for os. Men det er stadig vigtigt at forstå, hvordan det fungerer.,

    for At beregne prisen på en call-option, under Black Scholes-modellen, kan vi bruge følgende ligning:

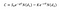
    Hvor:

    • S0 er aktiekursen;
    • e er den eksponentielle antal;
    • q er udbytteprocenten procentdel;
    • T er den periode (et år vil være T=1, mens seks måneder vil være T=0.,5);
    • N(d1) er delta call-option, som betyder, at den ændring i call pris over de skift i aktiekursen;
    • K er strike-pris;
    • r er den risikofrie rente, og
    • N(d2) er sandsynligheden for, at den fremtidige aktiekurs vil være højere end den pris, strejke, sandsynligheden for, at vi vil udnytte optionen.

    den Ene side er aktiekursen ganget med den kumulative standard normal fordeling af d1, og den anden — strike-prisen, der tilbagediskonteres til tiden T, og derefter ganget med den kumulative standard normal fordeling af d2.,

    Hvor kan vi beregne d1 og d2 med følgende formler:

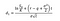
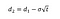
    Hvor σ er volatiliteten på afkastet af det underliggende aktiv.,

    Vi kan anvende den samme logik til en put-option:

    tilmeld dig vores Nyhedsbrev for at få et GRATIS Excel-Benchmark Analyse Skabelon

    Eksempel Black Scholes Beregning

    for bedre At illustrere konceptet bag Black Scholes-Modellen, vil vi tage et kig på følgende model. Vi starter med modelindgange., Som diskuteret ovenfor har vi brug for følgende seks variabler til at beregne opkalds-og indstillingsværdierne.

    Næste, vi vil beregne indstillinger’ parametre. Fra d1 får vi 0, 39 Fra vores modelantagelser.

    for At beregne det, skal vi blot overføre formlen for d1 til Excel.,

    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    Vi kan ansætte Call-Sætte Paritet regel til at kontrollere, om vores formler og beregninger er korrekte.

    Nu, at vi har vores model til at beregne Call-og Put-optioner priser, vi kan gå et skridt videre og se på, hvordan de forskellige input parametre påvirke resultaterne af vores model., Datatabellens funktionalitet i e .cel er et godt værktøj til at forberede nogle følsomhedsanalysetabeller til vores variabler. Du kan lære at bruge datatabeller i vores Følsomhedsanalyseartikel.

    lad os se på aktiekursen, hvis den ændrer sig fra 10 10 til 100 100, og hvordan det påvirker opkaldet og sætter værdier. Vi bemærker, at Call-optionen ikke har nogen værdi, indtil aktiekursen rammer 40 40. Vi ser det modsatte for Put-optionen, hvor dens værdi rammer nul, når aktiekursen går over 85 85.,

    Hvis vi forberede den samme følsomhed over bordet til den Pris, Strejke, vi kan observere det omvendte forhold. Når Strejkeprisen stiger, falder Opkaldsværdien, og Putværdien stiger.

    Lad os også tage et kig på den risiko, -gratis sats., Når det øges, øger dette også den krævede afkast. Derefter reducerer dette værdien af aktier. Vi bemærker et direkte forhold, når den risikofrie sats stiger, øges også Opkaldsindstillingsværdien, mens Put-Optionsværdien reducerer dens værdi.

    Efter den samme fremgangsmåde, du kan gå videre og se på resten af parametrene, og hvordan de påvirker Mulighed Værdier., Du kan do .nloade e .cel-modellen i slutningen af artiklen og gå over følsomhedsanalysen derinde.

    Du kan do .nloade eksempelmodellen i E .cel i den originale artikel.

    konklusion

    det er vigtigt at huske, at Black-Scholes-Merton-modellen er et teoretisk koncept. Vi bruger det til at forsøge at estimere markedets adfærd. Men når vi bruger resultaterne i vores beslutningsproces, er vi nødt til at forstå de underliggende antagelser i modellen, og hvordan den afviger fra virkeligheden.,formlen hjalp handel med optioner til at blive mere populær, da det får det til at se mindre ud som spil. I dag er forskellige modifikationer af sorte Scholes meget populære som grundlæggende strategier for risikokontrol, der er forbundet med volatilitet.

    Du kan vise din støtte ved at dele artiklen med kolleger og venner.