Naladěni Zesilovače

Inzeráty

typy zesilovačů, které jsme diskutovali zatím nemůže fungovat efektivně na rádiových frekvencích, a to i přesto, že jsou dobré na zvukové frekvence. Také zisk těchto zesilovačů je takový, že se nebude lišit podle frekvence signálu v širokém rozsahu., To umožňuje zesílení signálu stejně dobře v rozsahu frekvencí a neumožňuje výběr konkrétní požadované frekvence při odmítnutí ostatních frekvencí.

existuje tedy potřeba obvodu, který může vybrat i zesílit. Takže obvod zesilovače spolu s výběrem, jako je naladěný obvod, dělá vyladěný zesilovač.

co je naladěný zesilovač?

laděné zesilovače jsou zesilovače, které se používají pro účely ladění. Ladění znamená výběr., Mezi dostupnou sadou frekvencí, pokud je potřeba vybrat určitou frekvenci, při odmítnutí všech ostatních frekvencí se takový proces nazývá výběr. Tento výběr se provádí pomocí obvodu nazývaného jako vyladěný obvod.

když má obvod zesilovače své zatížení nahrazeno laděným obvodem,lze takový zesilovač nazvat jako vyladěný zesilovač. Základní naladěný zesilovač obvod vypadá, jak je znázorněno níže.

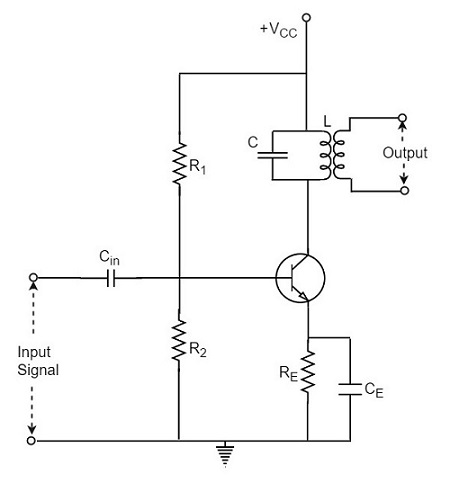
obvod tuneru není nic jiného než obvod LC, který se také nazývá jako rezonanční nebo tankový obvod. Vybírá frekvenci., Naladěný obvod je schopen zesílit signál přes úzké pásmo frekvencí, které jsou soustředěny na rezonanční frekvenci.

když reaktance induktoru vyrovnává reaktanci kondenzátoru, v naladěném obvodu při určité frekvenci může být taková frekvence nazývána jako rezonanční frekvence. To je označováno fr.,

vzorec pro rezonanční

$$2 \pi f_L = \frac{1}{2 \pi f_c}$$

$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$

Druhy Laděné Obvody

laděný obvod může být Série laděný obvod (Série rezonanční obvod) nebo Paralelní laděný obvod (paralelní rezonanční obvod) podle druhu jeho připojení k hlavnímu obvodu.

Série Laděný Obvod

induktor a kondenzátor zapojeny do série, aby se série laděný obvod, jak je znázorněno v následujícím schématu.,

při rezonanční frekvenci nabízí řada rezonančních obvodů nízkou impedanci, která umožňuje vysoký proud. Řada rezonanční obvod nabízí stále vysokou impedanci kmitočtů daleko od rezonanční frekvence.

Paralelní Laděný Obvod

cívky a kondenzátoru spojeny paralelně, aby paralelní laděný obvod, jak je znázorněno na obrázku dole.

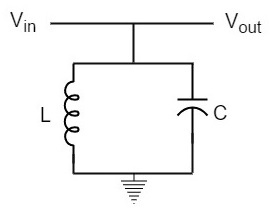
při rezonanční frekvenci nabízí paralelní rezonanční obvod vysokou impedanci, která přes něj neumožňuje vysoký proud., Paralelní rezonanční obvod nabízí stále nízkou impedanci kmitočtů daleko od rezonanční frekvence.

Vlastnosti Paralelní Laděný Obvod

frekvence, na které paralelní rezonanci dochází (tj. reaktivní složka zkratový proud dosáhne nuly) se nazývá rezonanční frekvence fr. Hlavní charakteristiky naladěného obvodu jsou následující.

Impedance

poměr napájecího napětí k proudu je impedance naladěného obvodu., Impedance nabízená obvodem LC je dána

$ $ \ frac{Supply\: voltage}{Line equation} = \ frac{v}{i}$

při rezonanci se proud linky zvyšuje, zatímco impedance klesá.

níže uvedený obrázek představuje impedanční křivku paralelního rezonančního obvodu.

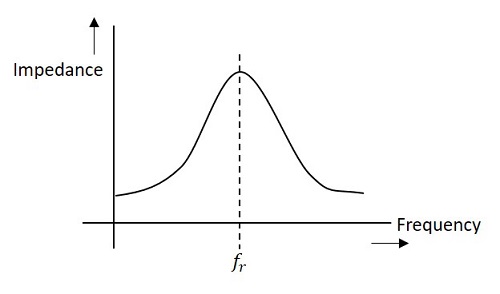
Impedance obvodu klesá pro hodnoty nad a pod rezonanční frekvencí fr. Proto je možný výběr určité frekvence a odmítnutí jiných frekvencí.,

To obtain an equation for the circuit impedance, let us consider

Line Current $I = I_L cos \phi$

$$\frac{V}{Z_r} = \frac{V}{Z_L} \times \frac{R}{Z_L}$$

$$\frac{1}{Z_r} = \frac{R}{Z_L^2}$$

$$\frac{1}{Z_r} = \frac{R}{L/C} = \frac{C R}{L}$$

Since, $Z_L^2 = \frac{L}{C}$

Therefore, circuit impedance Zr is obtained as

$$Z_R = \frac{L}{C R}$$

Thus at parallel resonance, the circuit impedance is equal to L/CR.,

zkratový Proud

Na paralelní rezonanční obvod nebo řádku proud I je dána aplikované napětí děleno obvodu impedance Zr tj.,

Aktuální $I = \frac{V}{Z_r}$

Kde $Z_r = \frac{L}{C-R}$

Protože Zr je velmi vysoká, line, proud bude velmi malý.

faktor kvality

pro paralelní rezonanční obvod určuje ostrost rezonanční křivky selektivitu. Čím menší je odpor cívky, tím ostřejší bude rezonanční křivka., Proto indukční reaktance a odpor cívky určují kvalitu naladěného obvodu.

poměr indukční reaktance cívky při rezonanci k jejímu odporu je známý jako faktor kvality. To je označen Q.

$$Q = \frac{X_L}{R} = \frac{2 \pi f_r L}{R}$$

čím vyšší Je hodnota Q, tím ostřejší rezonanční křivky a lepší selektivity bude.

výhody laděných zesilovačů

následující jsou výhody laděných zesilovačů.,

použití reaktivních komponent, jako jsou L A C, minimalizuje ztrátu výkonu, což činí vyladěné zesilovače efektivní.
selektivita a zesílení požadované frekvence je vysoká tím, že poskytuje vyšší impedanci při rezonanční frekvenci.
menší kolektor napájení VCC by to udělat, protože jeho malý odpor v paralelní laděný obvod.

je důležité si uvědomit, že tyto výhody nejsou použitelné, pokud existuje vysoké odporové zatížení kolektoru.,

Frekvenční odezva laděného zesilovače

aby byl zesilovač efektivní, měl by být jeho zisk vysoký. Tento zisk napětí závisí na β, vstupní impedanci a zatížení kolektoru. Zátěž kolektoru v naladěném zesilovači je vyladěný obvod.

napětí zisk tohoto zesilovače je dána tím,

Napětí zisk = $\frac{\beta Z_C}{Z_{v}}$

Kde ZC = efektivní zatížení kolektoru a Zin = vstupní impedance zesilovače.

hodnota ZC závisí na frekvenci vyladěného zesilovače., Protože ZC je maximální při rezonanční frekvenci, zisk zesilovače je maximální při této rezonanční frekvenci.

šířka Pásma

rozsah frekvencí, při které napětí zisk laděný zesilovač padá na 70,7% maximální zisk, se nazývá šířka Pásma.

rozsah frekvencí mezi f1 a f2 se nazývá jako šířka pásma naladěného zesilovače. Šířka pásma vyladěného zesilovače závisí na Q obvodu LC, tj. na ostrosti frekvenční odezvy. Hodnota Q a šířka pásma jsou nepřímo úměrné.,

níže uvedený obrázek podrobně popisuje šířku pásma a frekvenční odezvu naladěného zesilovače.

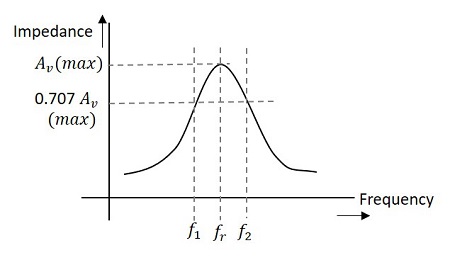
Vztah mezi Q a šířka Pásma

jakostní faktor Q, šířka pásma je definována jako poměr rezonanční frekvence pásma, tj.,

$$Q = \frac{f_r}{TH}$$

obecně platí, že praktické obvodu má Q hodnotu větší než 10.,

Za tohoto stavu, rezonanční frekvence při paralelní rezonanci je dána tím,