Un vector care are o mărime (în cât timp) și direcția:
Aici sunt doi vectori:

Acestea pot fi multiplicate folosind „Dot Produs” (a se vedea, de asemenea, Produs vectorial).,
putem calcula Produsul scalar a doi vectori astfel:

o · b = |a| × |b| × cos(θ)
Unde:
|o| este mărimea (lungimea) vector
|b| este mărimea (lungimea) vectorului b
θ este unghiul dintre a și b,
Deci, vom multiplica lungimea de ori lungimea b, apoi se înmulțește cu cosinusul unghiului dintre a și b,
SAU putem calcula în felul acesta:
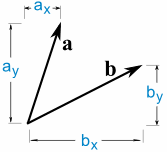
o · b = ax × bx + ay ×
Deci, vom multiplica lui x, se înmulțește y, apoi se adaugă.,
ambele metode funcționează!
și rezultatul este un număr (numit „scalar”, deci știm că nu este un vector).
Notă: puteți utiliza calculul Vectorialpentru a vă ajuta.
De ce cos (θ)?
OK, pentru a multiplica doi vectori are sens să se înmulțească lungimile lor împreună, dar numai atunci când acestea indică în aceeași direcție.,
Deci, vom face un „punct în aceeași direcție”, ca celelalte prin înmulțirea cu cos(θ):
 |
 |
|
| Vom lua componentă a unui care se află alături de b |
Ca o lumina stralucitoare pentru a vedea unde umbra se află |
APOI vom multiplica !,
unghiuri drepte
când doi vectori sunt în unghi drept unul față de celălalt, produsul punct este zero.aceasta poate fi o modalitate la îndemână de a afla dacă doi vectori sunt în unghi drept.
trei sau mai multe dimensiuni
toate acestea funcționează bine și în 3 (sau mai multe) dimensiuni. și poate fi de fapt foarte util!
am încercat un calcul de genul asta o dată, dar a lucrat toate în unghiuri și distanțe … a fost foarte greu, a implicat o mulțime de trigonometrie, și creierul meu rănit. Metoda de mai sus este mult mai ușoară.,
produs încrucișat
produsul punct dă un răspuns scalar (număr obișnuit) și este uneori numit produs scalar.
dar există și produsul încrucișat care dă un vector ca răspuns și este uneori numit produsul vectorial.

















Lasă un răspuns