Probabilitatea de rulare două zaruri cu șase fețe dotssuch ca 1, 2, 3, 4, 5 și 6 puncte de la fiecare moară.

Când două zaruri sunt aruncate simultan, astfel numărul de eveniment poate fi 62 = 36 pentru fiecare zar are de la 1 la 6 numărul de pe fețele sale. Apoi rezultatele posibile sunt prezentate în tabelul de mai jos.,
Probabilitate – Proba spațiu pentru două zaruri (rezultate):
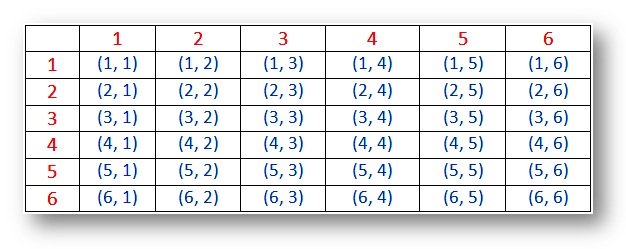
Notă:
(i) rezultatele (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) și (6, 6) sunt numite dublete.(ii) perechea (1, 2) și (2, 1) sunt rezultate diferite.
probleme elaborate care implică probabilitatea de rulare două zaruri:
1. Două zaruri sunt rulate. Fie A, B, C evenimentele de a obține o sumă de 2, o sumă de 3 și, respectiv, o sumă de 4., Apoi, arată că
(i) O este un simplu eveniment
(ii), B și C sunt compuse evenimente
(iii) a și B sunt mutual exclusive
Soluție:
în mod Clar, avem
A = {(1, 1)}, B = {(1, 2), (2, 1)} și C = {(1, 3), (3, 1), (2, 2)}.
(i) deoarece A constă dintr-un singur punct de probă, este un eveniment simplu.(ii) deoarece ambele B și C conțin mai mult de un punct de probă, fiecare dintre ele este un eveniment compus.
(iii) deoarece A ∩ B = ∅, A și B se exclud reciproc.
2. Două zaruri sunt rulate., A este cazul în care suma numerelor afișate pe cele două zaruri este 5, și B este cazul în care cel puțin unul dintre zaruri apare un 3.
cele două evenimente (i) se exclud reciproc, (ii) sunt exhaustive? Oferiți argumente în sprijinul răspunsului dvs.când două zaruri sunt rulate, avem n (S) = (6 × 6) = 36.
Acum, O = {(1, 4), (2, 3), (4, 1), (3, 2)}, și
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.prin urmare, A și B nu se exclud reciproc.,
(ii) de asemenea, A ∪ B ≠ S.
prin urmare, a și B nu sunt evenimente exhaustive.mai multe exemple legate de întrebările privind probabilitățile pentru aruncarea a două zaruri.
3. Două zaruri sunt aruncate simultan.,) obtinerea unui dublet
(v) obtinerea unei sume de 8
(vi) obtinerea suma divizibil cu 5
(vii) obtinerea suma de cel putin 11
(viii) obtinerea un multiplu de 3, ca suma
(ix) obtinerea unui total de cel putin 10
(x) obținerea unui număr ca sumă
(xi) obtinerea un prim număr ca sumă
(xii) obtinerea unui dublet de numere, chiar
(xiii) obtinerea unui multiplu de 2 pe o moară și un multiplu de 3 pe de altă moară
Soluție:
Două zaruri sunt aruncate simultan, fiind numărul 1, 2, 3, 4, 5 și 6 de pe fețele lor., Știm că într-o singură aruncare a două zaruri diferite, numărul total de rezultate posibile este (6 × 6) = 36.
(i) Noțiuni de bază șase ca un produs:
să E1 = eveniment de a obține șase ca un produs. Numărul al cărui produs este de șase va fi E1 = = 4
prin Urmare, probabilitatea de a avea șase ca un produs
Numărul de rezultate favorabile
P(E1) = numărul Total de rezultate posibile
= 4/36
= 1/9
(ii) obtinerea suma ≤ 3:
E2 = eveniment de a obține suma ≤ 3., Numărul a căror sumă ≤ 3 va fi E2 = = 3
prin Urmare, probabilitatea de a avea ‘suma ≤ 3’
Numărul de rezultate favorabile
P(E2) = numărul Total de rezultate posibile
= 3/36
= 1/12
(iii) obtinerea suma de maximum 10:
Să E3 = eveniment de a obține suma ≤ 10. Numărul a căror sumă ≤ 10 va fi E3 =
= 33
prin Urmare, probabilitatea de a avea ‘suma ≤ 10’
Numărul de rezultate favorabile
P(E3) = numărul Total de rezultate posibile
= 33/36
= 11/12
(iv)obtinerea unui dublet:Să E4 = eveniment de obtinerea unui dublet., Numărul care dublet va fi E4 = = 6
prin Urmare, probabilitatea de a avea un dublet’
Numărul de rezultate favorabile
P(E4) = numărul Total de rezultate posibile
= 6/36
= 1/6
(v)obtinerea unei sume de 8:
E5 = eveniment de a obține o sumă de 8. Numărul care este o sumă de 8 va fi E5 = = 5
prin Urmare, probabilitatea de a avea o suma de 8′
Numărul de rezultate favorabile
P(E5) = numărul Total de rezultate posibile
= 5/36
(vi)obtinerea suma divizibil cu 5:
Să E6 = eveniment de a obține suma divizibil cu 5., Numărul a cărui sumă divizibil cu 5 va fi E6 = = 7
prin urmare, probabilitatea ofgetting ‘suma divizibil cu 5’
Numărul de rezultate favorabile
P (E6)= numărul Total de rezultat posibil
= 7/36
(vii) obtinerea suma de atleast 11:
fie E7 = eveniment de a obține suma de atleast 11. Evenimentele din suma de cel putin 11 va fi E7 = = 3
prin Urmare, probabilitatea de a avea ‘suma de cel putin 11’
Numărul de rezultate favorabile
P(E7) = numărul Total de rezultate posibile
= 3/36
= 1/12
(viii) obtinerea amultiple de 3 ca suma:
Să E8 = eveniment de a obține un multiplu de 3, ca sumă., Evenimentele de un multiplu de 3, ca suma va fi E8 = = 12
prin Urmare, probabilitatea de a avea un multiplu de 3, ca suma’
Numărul de rezultate favorabile
P(E8) = numărul Total de rezultate posibile
= 12/36
= 1/3
(ix) obtinerea unui totalof cel putin 10:
Să E9 = eveniment de a obține un total de cel putin 10., Evenimentele dintr-un total de cel putin 10 va fi E9 = = 6
prin Urmare, probabilitatea de a avea un total de cel putin 10′
Numărul de rezultate favorabile
P(E9) = numărul Total de rezultate posibile
= 6/36
= 1/6
(x) obtinerea unui evennumber ca suma:
Să E10 = eveniment de a obține chiar și un număr ca sumă., Evenimentele de un număr ca sumă va fi E10 = = 18
prin Urmare, probabilitatea de a avea un număr par ca suma
Numărul de rezultate favorabile
P(E10) = numărul Total de rezultate posibile
= 18/36
= 1/2
(xi) obtinerea unui primenumber ca suma:
Să E11 = eveniment de a obține un prim număr ca sumă., Evenimentele din prim număr ca sumă va fi E11 = = 15
prin Urmare, probabilitatea de a avea un prim număr ca sumă de’
Numărul de rezultate favorabile
P(E11) = numărul Total de rezultate posibile
= 15/36
= 5/12
(xii) obtinerea adoublet de numere:
Să E12 = eveniment de a obține un dublet de numere., Evenimentele de un dublet de numere, chiar va fi E12 = = 3
prin Urmare, probabilitatea de a avea un dublet de numere, chiar’
Numărul de rezultate favorabile
P(E12) = numărul Total de rezultate posibile
= 3/36
= 1/12
(xiii) obtinerea amultiple de 2 pe o moară și un multiplu de 3 pe de altă moară:
Să E13 = eveniment de a obține un multiplu de 2, pe o moară și un multiplu de 3 pe de altă moară., Evenimentele de mai multe de 2 pe o moară și un multiplu de 3 pe de altă muri va fi E13 = = 11
prin Urmare, probabilitatea de a avea un multiplu de 2, pe o moară și un multiplu de 3 pe de altă mor’
Numărul de rezultate favorabile
P(E13) = numărul Total de rezultate posibile
= 11/36
4. Două bucăți sunt aruncate. Găsiți (i) cotele în favoarea obținerii sumei 5 și (ii) theodds împotriva obținerii sumei 6.
soluție:
știm că într-o singură aruncare a două matrițe, numărul totalde rezultate posibile este (6 × 6) = 36.
să fie spațiul de probă. Apoi, n ( S) = 36.,
(i) cotele în favoarea obținerii sumei 5:
fie E1 evenimentul obținerii sumei 5. Apoi,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)} rin urmare, p(E1) = n (E1) / n(s) = 4/36 = 1/9
⇒ cote în favoarea E1 = P (E1)/ = (1/9)/(1 – 1/9) = 1/8.(ii) șansele de a obține suma 6:fie E2 evenimentul de a obține suma 6. Apoi,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)} rin urmare, p(E2) = n (E2) /n(s) = 5/36
⇒ cote împotriva E2 = / P (E2) = (1 – 5/36)/(5/36) = 31/5.
5., Două zaruri, unul albastru și unul portocaliu, sunt rulate simultan. Găsiți probabilitatea de a obține
(i) numere egale pe ambele
(ii) două numere care apar pe ele a căror sumă este 9.,
Rezolvare:
rezultatele posibile sunt
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
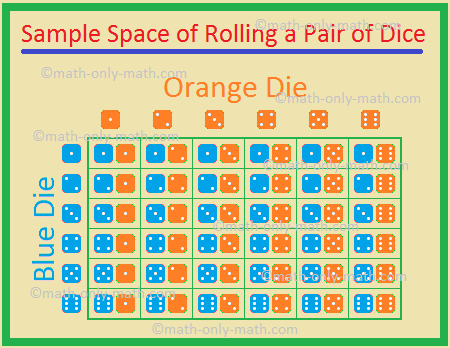
prin Urmare, numărul total de rezultate posibile = 36.,
(i) Numărul de rezultate favorabile pentru eveniment e
= numărul de rezultate având numere egale pe ambele zaruri
= 6 .
Deci, prin definiție, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Numărul de rezultate favorabile pentru cazul F
= Numărul de rezultate în care două numere care apar pe ele au suma 9
= 4 .
astfel, prin definiție, P (F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).aceste exemple vor ajutanoi pentru a rezolva diferite tipuri de probleme bazate pe probabilitatea de rularedouă zaruri.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Lasă un răspuns